/Szkoła średnia/Zadania maturalne/Matura 2020
Egzamin Maturalny
z Matematyki (stara formuła)
poziom podstawowy 9 czerwca 2020 Czas pracy: 170 minut
Zadania zamknięte
Wartość wyrażenia 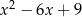 dla
dla 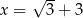 jest równa
jest równa
A) 1 B) 3 C) 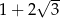 D)
D) 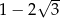
Liczba 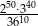 jest równa
jest równa
A) 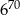 B)
B) 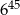 C)
C) 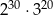 D)
D) 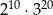
Liczba 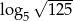 jest równa
jest równa
A)  B) 2 C) 3 D)
B) 2 C) 3 D) 
Cenę  pewnego towaru obniżono o 20% i otrzymano cenę
pewnego towaru obniżono o 20% i otrzymano cenę 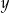 . Aby przywrócić cenę
. Aby przywrócić cenę  , nową cenę
, nową cenę 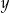 należy podnieść o
należy podnieść o
A) o 25% B) o 20% C) o 15% D) o 12%
Zbiorem wszystkich rozwiązań nierówności 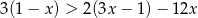 jest przedział
jest przedział
A) 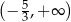 B)
B) 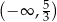 C)
C) 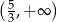 D)
D) 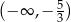
Suma wszystkich rozwiązań równania 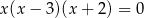 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Informacja do zadań 7 – 9
Funkcja kwadratowa 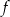 jest określona wzorem
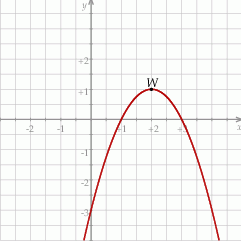
jest określona wzorem 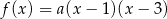 . Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Wierzchołkiem tej paraboli jest punkt
. Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Wierzchołkiem tej paraboli jest punkt 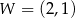 .
.
Współczynnik  we wzorze funkcji
we wzorze funkcji 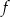 jest równy
jest równy
A) 1 B) 2 C) 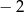 D)
D) 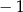
Największa wartość funkcji 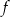 w przedziale
w przedziale 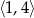 jest równa
jest równa
A) 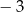 B) 0 C) 1 D) 2
B) 0 C) 1 D) 2
Osią symetrii paraboli będącej wykresem funkcji 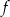 jest prosta o równaniu
jest prosta o równaniu
A) 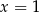 B)
B) 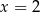 C)
C) 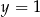 D)
D) 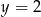
Równanie 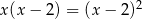 w zbiorze liczb rzeczywistych
w zbiorze liczb rzeczywistych
A) nie ma rozwiązań
B) ma dokładnie jedno rozwiązanie: 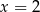
C) ma dokładnie jedno rozwiązanie: 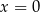
D) ma dwa różne rozwiązania: 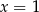 i
i 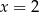
Na rysunku przedstawiono fragment wykresu funkcji liniowej 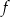 określonej wzorem
określonej wzorem 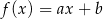 .
.
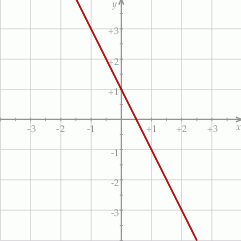
Współczynniki  oraz
oraz 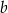 we wzorze funkcji
we wzorze funkcji 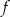 spełniają zależność
spełniają zależność
A) 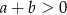 B)
B) 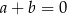 C)
C) 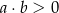 D)
D) 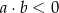
Funkcja 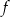 jest określona wzorem
jest określona wzorem 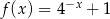 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Liczba
. Liczba 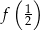 jest równa
jest równa
A) 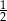 B)
B)  C) 3 D) 17
C) 3 D) 17
Proste o równaniach 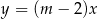 oraz
oraz 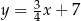 są równoległe. Wtedy
są równoległe. Wtedy
A) 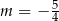 B)
B) 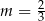 C)
C) 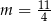 D)
D) 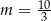
Ciąg 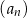 jest określony wzorem
jest określony wzorem 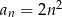 dla
dla 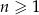 . Różnica
. Różnica 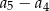 jest równa
jest równa
A) 4 B) 20 C) 36 D) 18
W ciągu arytmetycznym 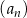 , określonym dla
, określonym dla 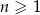 , czwarty wyraz jest równy 3, a różnica tego ciągu jest równa 5. Suma
, czwarty wyraz jest równy 3, a różnica tego ciągu jest równa 5. Suma 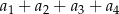 jest równa
jest równa
A) 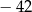 B)
B) 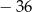 C)
C) 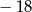 D) 6
D) 6
Punkt 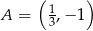 należy do wykresu funkcji liniowej
należy do wykresu funkcji liniowej 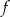 określonej wzorem
określonej wzorem 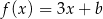 . Wynika stąd, że
. Wynika stąd, że
A) 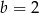 B)
B) 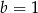 C)
C) 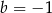 D)
D) 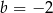
Punkty 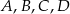 leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie 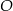 . Kąt środkowy
. Kąt środkowy 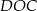 ma miarę
ma miarę 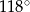 (zobacz rysunek).
(zobacz rysunek).
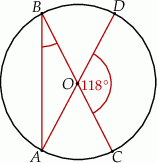
Miara kąta 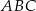 jest równa
jest równa
A) 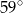 B)
B) 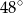 C)
C) 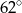 D)
D) 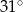
Prosta przechodząca przez punkty 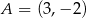 i
i 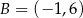 jest określona równaniem
jest określona równaniem
A) 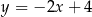 B)
B) 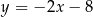 C)
C) 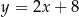 D)
D) 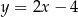
Dany jest trójkąt prostokątny o kątach ostrych  i
i 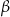 (zobacz rysunek).
(zobacz rysunek).
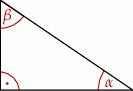
Wyrażenie 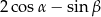 jest równe
jest równe
A) 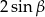 B)
B) 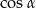 C) 0 D) 2
C) 0 D) 2
Punkt 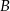 jest obrazem punktu
jest obrazem punktu 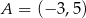 w symetrii względem początku układu współrzędnych. Długość odcinka
w symetrii względem początku układu współrzędnych. Długość odcinka 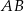 jest równa
jest równa
A) 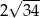 B) 8 C)
B) 8 C) 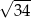 D) 12
D) 12
Ile jest wszystkich dwucyfrowych liczb naturalnych utworzonych z cyfr: 1, 3, 5, 7, 9, w których cyfry się nie powtarzają?
A) 10 B) 15 C) 20 D) 25
Pole prostokąta 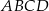 jest równe 90. Na bokach
jest równe 90. Na bokach 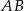 i
i 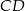 wybrano – odpowiednio – punkty
wybrano – odpowiednio – punkty 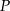 i
i 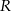 , takie, że
, takie, że 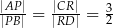 (zobacz rysunek)
(zobacz rysunek)
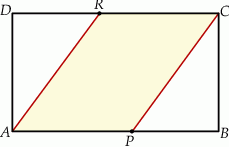
Pole czworokąta 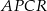 jest równe
jest równe
A) 36 B) 40 C) 54 D) 60
Cztery liczby: 2, 3,  , 8, tworzące zestaw danych, są uporządkowane rosnąco. Mediana tego zestawu czterech danych jest równa medianie zestawu pięciu danych: 5, 3, 6, 8, 2. Zatem
, 8, tworzące zestaw danych, są uporządkowane rosnąco. Mediana tego zestawu czterech danych jest równa medianie zestawu pięciu danych: 5, 3, 6, 8, 2. Zatem
A) 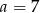 B)
B) 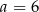 C)
C) 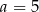 D)
D) 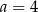
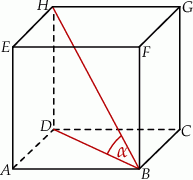
Dany jest sześcian 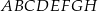 . Sinus kąta
. Sinus kąta  nachylenia przekątnej
nachylenia przekątnej 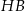 tego sześcianu do płaszczyzny podstawy
tego sześcianu do płaszczyzny podstawy 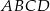 (zobacz rysunek) jest równy
(zobacz rysunek) jest równy
A) 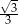 B)
B) 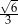 C)
C) 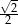 D)
D) 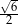
Dany jest stożek o objętości 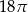 , którego przekrojem osiowym jest trójkąt
, którego przekrojem osiowym jest trójkąt 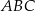 (zobacz rysunek). Kąt
(zobacz rysunek). Kąt 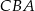 jest kątem nachylenia tworzącej
jest kątem nachylenia tworzącej 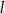 tego stożka do płaszczyzny jego podstawy. Tangens kąta
tego stożka do płaszczyzny jego podstawy. Tangens kąta 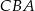 jest równy 2.
jest równy 2.
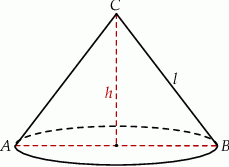
Wynika stąd, że wysokość 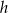 tego stożka jest równa
tego stożka jest równa
A) 12 B) 6 C) 4 D) 2
Zadania otwarte
Rozwiąż nierówność 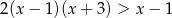 .
.
Rozwiąż równanie 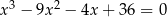 .
.
Wykaż, że dla każdych dwóch różnych liczb rzeczywistych  i
i 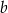 prawdziwa jest nierówność
prawdziwa jest nierówność
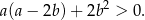
Trójkąt 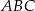 jest równoboczny. Punkt
jest równoboczny. Punkt 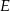 leży na wysokości
leży na wysokości 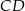 tego trójkąta oraz
tego trójkąta oraz 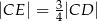 . Punkt
. Punkt 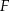 leży na boku
leży na boku 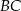 i odcinek
i odcinek 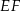 jest prostopadły do
jest prostopadły do 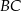 (zobacz rysunek).
(zobacz rysunek).
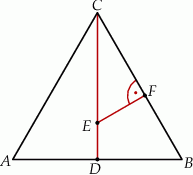
Wykaż, że 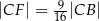 .
.
Rzucamy dwa razy symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek – od jednego oczka do sześciu oczek. Oblicz prawdopodobieństwo zdarzenia 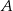 polegającego na tym, że co najmniej jeden raz wypadnie ścianka z pięcioma oczkami.
polegającego na tym, że co najmniej jeden raz wypadnie ścianka z pięcioma oczkami.
Kąt  jest ostry i spełnia warunek
jest ostry i spełnia warunek 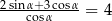 . Oblicz tangens kąta
. Oblicz tangens kąta  .
.
Dany jest kwadrat 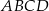 , w którym
, w którym 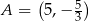 . Przekątna
. Przekątna 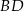 tego kwadratu jest zawarta w prostej o równaniu
tego kwadratu jest zawarta w prostej o równaniu 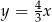 . Oblicz współrzędne punktu przecięcia przekątnych
. Oblicz współrzędne punktu przecięcia przekątnych 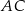 i
i 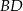 oraz pole kwadratu
oraz pole kwadratu 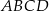 .
.
Wszystkie wyrazy ciągu geometrycznego 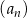 , określonego dla
, określonego dla 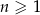 , są dodatnie. Wyrazy tego ciągu spełniają warunek
, są dodatnie. Wyrazy tego ciągu spełniają warunek 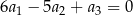 . Oblicz iloraz
. Oblicz iloraz 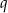 tego ciągu należący do przedziału
tego ciągu należący do przedziału 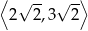 .
.
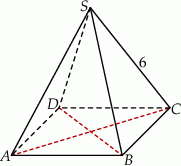
Dany jest ostrosłup prawidłowy czworokątny 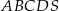 , którego krawędź boczna ma długość 6 (zobacz rysunek). Ściana boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem, którego tangens jest równy
, którego krawędź boczna ma długość 6 (zobacz rysunek). Ściana boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem, którego tangens jest równy 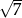 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.