/Szkoła podstawowa/Egzamin ósmoklasisty/Egzamin 2020/Próbne testy
Próbny Egzamin Ósmoklasisty
z Matematyki Zestaw przygotowany przez serwis zadania.info 14 marca 2020 Czas pracy: 100 minut
Na rysunku przedstawiono cztery kartki ze starych kalendarzy – dwie z nich pochodzą z kalendarza z roku 1982, jedna z roku 1981, jedna z roku 1983.

Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| W 1982 roku 4 lipca wypadł sobotę. | P | F |
| W 1981 roku 15 czerwca wypadł w poniedziałek. | P | F |
Liczbę  zaokrąglono do najbliższej liczby całkowitej i otrzymano
zaokrąglono do najbliższej liczby całkowitej i otrzymano 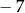 . O liczbie
. O liczbie 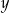 wiadomo, że jej odległość od
wiadomo, że jej odległość od  na osi liczbowej jest równa 7,35.
na osi liczbowej jest równa 7,35.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Jeżeli 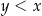 , to liczba , to liczba 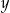 jest na pewno mniejsza niż jest na pewno mniejsza niż 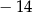 . . | P | F |
Jeżeli 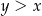 , to liczba , to liczba 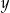 jest na pewno dodatnia. jest na pewno dodatnia. | P | F |
W tabeli zapisano trzy wyrażenia.
| I | 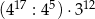 |
| II | 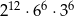 |
| III | 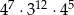 |
Które z tych wyrażeń są równe 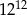 ?
?
Wybierz właściwą odpowiedź spośród podanych.
A) Tylko I i III. B) Tylko II i III. C) Tylko I. D) Tylko III.
Dane są liczby 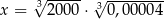 i
i 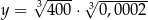 . Czy liczby
. Czy liczby  i
i 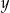 są równe? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
są równe? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
| Tak | Nie |
| ponieważ | |
| A) | 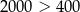 i i 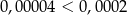 . . |
| B) | 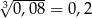 . . |
| C) | 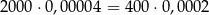 . . |
Kulki magnetyczne są sprzedawane w zestawach w kształcie sześcianu o krawędzi składającej się z 6 kulek (zobacz rysunek).

Kamil kupił 3 takie zestawy kulek magnetycznych, a następnie zbudował z nich wszystkich pewną liczbę sześcianów o krawędzi składającej się z 3 kulek.
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Kamil kupił w sumie A/B kulek magnetycznych.
A) 648 B) 216
Kamil zbudował C/D sześciany o krawędzi składającej się z 3 kulek.
C) 24 D) 72
W galerii handlowej rozdawano kupony rabatowe pozwalające kupić bilet do kina za cenę o 25% niższą od ceny normalnej. Wojtek kupił 2 bilety normalne i 2 bilety z rabatem za łączną kwotę 63 zł. Patrycja kupiła 1 bilet normalny i 3 bilety z rabatem na ten sam seans filmowy.
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Wartość rabatu udzielonego na zakup jednego biletu była równa A/B .
A) 4,5 zł B) 5,5 zł
Patrycja zapłaciła za bilety do kina C/D .
C) 58,50 zł D) 47,50 zł
Pewnym samolotem podróżowało więcej niż 100 pasażerów. Dwie trzecie z nich zapłaciło za przewóz bagażu po 400 zł, a pozostali – po 100 zł.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Średnia arytmetyczna opłat za przewóz bagażu w tym samolocie jest równa 200 zł. | P | F |
| Gdyby z podróży zrezygnowały trzy osoby, z których jedna zapłaciła za bagaż 100 zł, a dwie zapłaciły za bagaż po 400 zł, to średnia arytmetyczna opłat za przewóz bagażu w tym samolocie się nie zmieni. | P | F |
Na rysunku przedstawiono wzór jaki został naniesiony na prostokąt 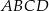 . Wzór ten składa się z 7 prostokątów o bokach
. Wzór ten składa się z 7 prostokątów o bokach  i
i  .
.
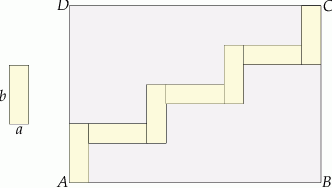
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Pole prostokąta 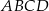 jest równe
jest równe
A) 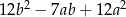 B)
B) 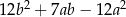 C)
C) 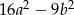 D)
D) 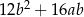
W układzie współrzędnych wyznaczono odcinek o końcach w punktach  ,
,  i środku w punkcie
i środku w punkcie 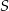 . Punkt
. Punkt 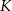 ma współrzędne
ma współrzędne 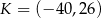 , a punkt
, a punkt 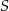 współrzędne
współrzędne 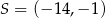 .
.
Na którym rysunku zacieniowana część płaszczyzny zawiera punkt 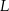 ? Wybierz właściwą odpowiedź spośród podanych.
? Wybierz właściwą odpowiedź spośród podanych.
Na rysunku przedstawiono trzy figury: prostokąt, kwadrat, trójkąt.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
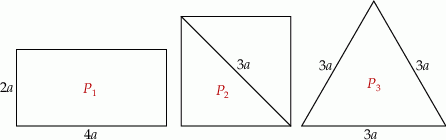
Spośród przedstawionych figur największe pole ma figura 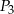 . . | P | F |
Spośród podanych figur najmniejsze pole ma figura 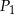 . . | P | F |
Na rysunku przedstawiono trzy trójkąty.
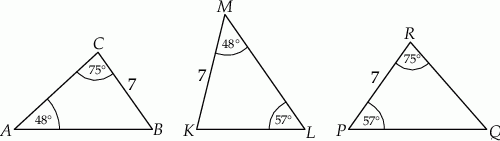
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Na podstawie informacji przedstawionych na rysunku można stwierdzić, że
A) trójkąt 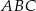 jest przystający do trójkąta
jest przystający do trójkąta 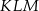 .
.
B) trójkąt 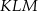 jest przystający do trójkąta
jest przystający do trójkąta 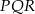 .
.
C) trójkąt 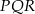 jest przystający do trójkąta
jest przystający do trójkąta 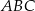 .
.
D) wszystkie trójkąty są do siebie przystające.
Szklane naczynie, którego podstawa ma kształt prostopadłościanu o wymiarach 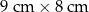 zostało wypełnione wodą do wysokości 12 cm. Następnie woda ta została przelana do drugiego szklanego naczynia, którego podstawa ma wymiary
zostało wypełnione wodą do wysokości 12 cm. Następnie woda ta została przelana do drugiego szklanego naczynia, którego podstawa ma wymiary 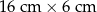 .
.
Do jakiej wysokości sięga woda w drugim naczyniu? Wybierz odpowiedź spośród podanych.
A) 9 cm B) 11 cm C) 10 cm D) 12 cm
Odcinek 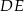 jest równoległy do podstawy
jest równoległy do podstawy 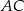 trójkąta równoramiennego
trójkąta równoramiennego 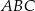 (zobacz rysunek).
(zobacz rysunek).
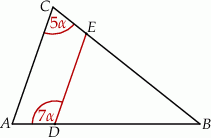
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Kąt 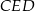 ma miarę A/B .
ma miarę A/B .
A) 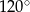 B)
B) 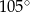
Kąt 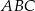 ma miarę C/D .
ma miarę C/D .
C) 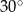 D)
D) 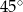
Na rysunku przedstawiono trapez równoramienny o podstawach 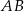 i
i 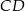 . Dane są długości odcinków
. Dane są długości odcinków 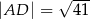 ,
, 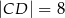 ,
, 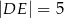 .
.
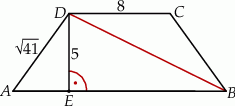
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Długość przekątnej 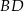 jest równa
jest równa
A) 13 B) 14 C) 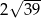 D)
D) 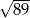
Na rysunku przedstawiono fragment siatki ostrosłupa prawidłowego trójkątnego.
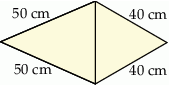
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Suma długości wszystkich krawędzi tego ostrosłupa jest równa
A) 560 cm B) 360 cm C) 260 cm D) 270 cm
W każdym z dwóch pudełek są tylko kule białe i czarne. Prawdopodobieństwo wylosowania kuli czarnej z pierwszego pudełka jest równe 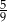 . W drugim pudełku jest dwa razy więcej kul białych i trzy razy więcej kul czarnych niż w pierwszym pudełku. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. W drugim pudełku jest dwa razy więcej kul białych i trzy razy więcej kul czarnych niż w pierwszym pudełku. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| W pierwszym pudełku są 4 kule białe. | P | F |
Prawdopodobieństwo wylosowania kuli białej z drugiego pudełka jest równe 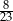 . . | P | F |
Cegielnia sprzedaje cegły pakowane w paletach po 330 sztuk. Gdyby ułożyć wszystkie cegły z jednej palety jedna za drugą, to łączna ich długość wyniosłaby 82,5 m. Ile cegieł należałoby ułożyć jedna za drugą, aby ich łączna długość wynosiła 1,5 km? Ile palet należałoby zamówić, aby kupić taką liczbę cegieł?
Samochód ciężarowy przebył 70% trasy w czasie 330 minut, a na pokonanie pozostałych 156 km potrzebował 150 minut. Z jaką średnią prędkością przebył całą trasę ten samochód ciężarowy? Prędkość wyraź w kilometrach na godzinę.
Podstawa ostrosłupa prawidłowego czworokątnego ma pole 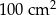 , a jego pole powierzchni bocznej jest równe
, a jego pole powierzchni bocznej jest równe 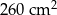 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Ada wycięła z kartonu równoległobok 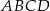 o bokach
o bokach 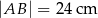 ,
, 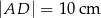 i polu równym
i polu równym 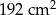 (rysunek I). Następnie rozcięła ten równoległobok na dwie pary przystających trapezów i złożyła z tych trapezów wielokąt przedstawiony na rysunku II. Od tego wielokąta odcięła dolną część wzdłuż jego przekątnej
(rysunek I). Następnie rozcięła ten równoległobok na dwie pary przystających trapezów i złożyła z tych trapezów wielokąt przedstawiony na rysunku II. Od tego wielokąta odcięła dolną część wzdłuż jego przekątnej 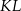 i otrzymała w ten sposób wielokąt przedstawiony na rysunku III.
i otrzymała w ten sposób wielokąt przedstawiony na rysunku III.
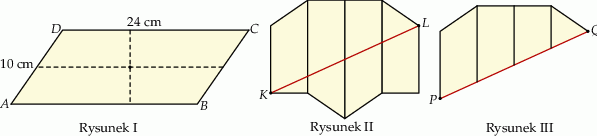
Oblicz obwód wielokąta z rysunku III.
Pewna szkoła podstawowa wzięła udział w programie przesiewowych badań słuchu. Pierwszego dnia przebadano 1/5 wszystkich uczniów szkoły. Drugiego dnia przebadano 1/3 pozostałych uczniów. Trzeciego dnia przebadano jeszcze 96 uczniów, a pozostałych 288 uczniów nie wzięło udziału w badaniu. Ilu uczniów uczy się w tej szkole podstawowej?

