/Szkoła podstawowa/Egzamin ósmoklasisty/Egzamin 2021
Próbny Egzamin Ósmoklasisty
z Matematyki Zestaw przygotowany przez serwis zadania.info 15 maja 2021 Czas pracy: 100 minut
Na diagramie przedstawiono wyniki sprawdzianu z matematyki przeprowadzonego w klasie VIIIc. Za rozwiązanie wszystkich zadań można było uzyskać maksymalnie 30 punktów, ale nikt nie zdobył więcej niż 25 punktów oraz nikt nie otrzymał mniej niż 10 punktów.
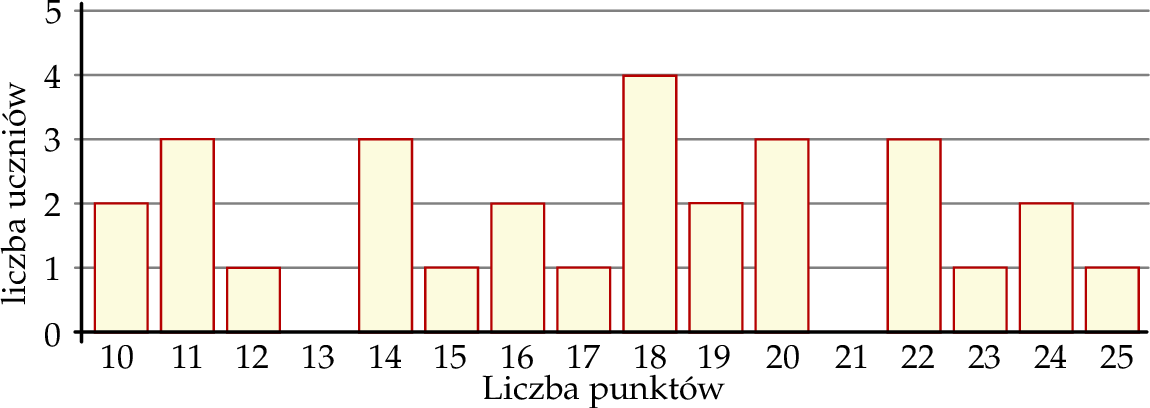
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Wynik powyżej 50% punktów możliwych do zdobycia uzyskało A/B uczniów.
A) 19 B) 20
Dokładnie 12 uczniów uzyskało wynik C/D punktów możliwych do zdobycia.
C) powyżej 60% D) poniżej 40%
Wartość wyrażenia 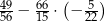 jest równa
jest równa
A) 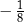 B)
B)  C)
C) 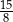 D) 2
D) 2
Firma „Poziomka” produkuje napój owocowy mieszając przecier owocowy i wodę w stosunku 2 : 7. Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Z 400 litrów przecieru owocowego można wyprodukować A/B napoju owocowego.
A) 1400 B) 1800
Do wyprodukowania 450 litrów napoju owocowego potrzeba C/D litrów wody.
C) 280 D) 350
Dwaj kolarze pokonali linię mety wyścigu kolarskiego z tą samą prędkością 54 km/h, przy czym pierwszy z nich minął linię mety o pół sekundy wcześniej niż drugi kolarz. O ile metrów pierwszy kolarz wyprzedzał drugiego podczas przekraczania linii mety?
Wybierz odpowiedź spośród podanych.
A) 7,5 m B) 15 m C) 10 m D) 9 m
Na przedstawionym poniżej fragmencie osi liczbowej oznaczono cztery punkty: 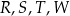 . Współrzędne punktów
. Współrzędne punktów 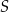 i
i 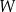 są równe 283 i 419. Odcinek
są równe 283 i 419. Odcinek 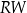 jest podzielony na sześć równych części.
jest podzielony na sześć równych części.

Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Współrzędne punktów 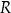 i i 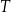 różnią się o 102. różnią się o 102. | P | F |
Współrzędna punktu 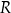 jest równa 215. jest równa 215. | P | F |
Dane są trzy liczby
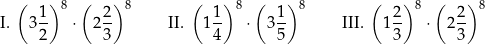
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Tylko jedna wśród liczb: I, II i III jest całkowita. | P | F |
| Liczba II jest większa od pozostałych dwóch liczb. | P | F |
Na diagramie przedstawiono wzrost (w centymetrach) ośmiu koszykarzy.

Ilu z tych zawodników ma wzrost mniejszy niż średni wzrost wszystkich zawodników przedstawionych na diagramie? Wybierz właściwą odpowiedź spośród podanych.
A) 2 B) 3 C) 4 D) 5
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Wartość wyrażenia 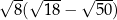 jest równa
jest równa
A) 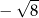 B)
B) 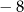 C)
C) 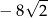 D)
D) 
Na rysunku przedstawiono siatkę graniastosłupa prawidłowego trójkątnego oraz zaznaczono na niej środki niektórych z jego krawędzi.
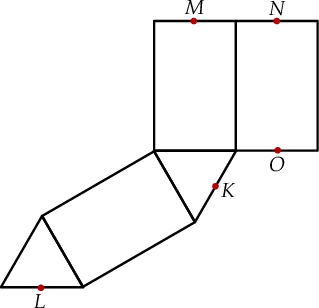
Dokończ zdanie. Wybierz odpowiedź spośród podanych.
Po złożeniu graniastosłupa z tej siatki punkt 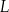 pokryje się z punktem
pokryje się z punktem
A) 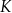 B)
B) 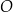 C)
C) 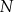 D)
D) 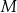
Dany jest wzór: 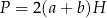 opisujący pole powierzchni bocznej graniastosłupa prostego czworokątnego o wysokości
opisujący pole powierzchni bocznej graniastosłupa prostego czworokątnego o wysokości 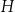 i krawędziach podstawy równych:
i krawędziach podstawy równych: 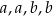 .
.
Którym równaniem opisano 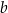 wyznaczone poprawnie z tego wzoru? Wybierz właściwą odpowiedź spośród podanych.
wyznaczone poprawnie z tego wzoru? Wybierz właściwą odpowiedź spośród podanych.
A) 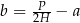 B)
B) 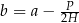 C)
C) 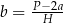 D)
D) 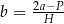
Krótsze ramię trapezu prostokątnego ma długość 4 cm, a jego krótsza podstawa ma długość 3 cm. Kąt ostry tego trapezu ma miarę 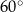 . Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Wysokość tego trapezu ma długość 4 cm. | P | F |
Pole tego trapezu jest równe 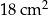 . . | P | F |
Na kartce w kratkę Tomek narysował według pewnej reguły cztery łamane (patrz rysunek).
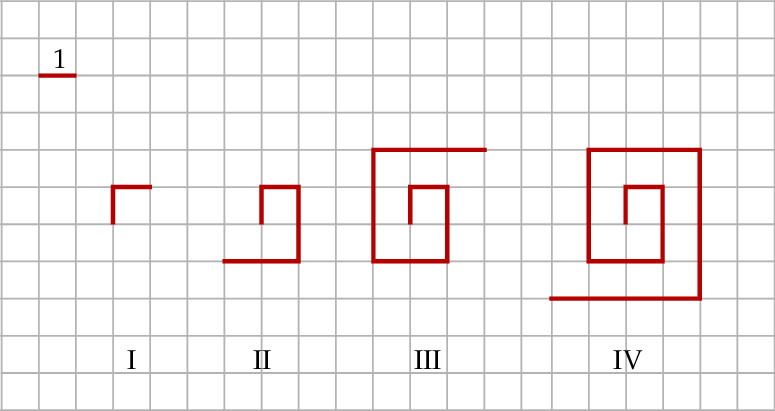
Długości tych łamanych zapisał w tabeli.
| Numer łamanej | I | II | III | IV |
| Długość łamanej | 2 | 6 | 12 | 20 |
Kolejne łamane – od numeru V – Tomek rysował zgodnie z tą samą regułą.
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Łamana o długości 56 ma numer A/B .
A) VI B) VII
Łamana o numerze VIII ma długość C/D .
C) 72 D) 80
Bilet ulgowy do cyrku jest o 40% tańszy od biletu normalnego. Tata Jacka za 2 bilety normalne i 3 ulgowe zapłacił 228 zł.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Mama Patrycji za 1 bilet normalny i 2 ulgowe musi zapłacić 132 zł. | P | F |
| Bilet normalny jest droższy od ulgowego o 26 zł. | P | F |
Dany jest trójkąt równoboczny 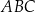 o boku długości 8 cm. W tym trójkącie poprowadzono wysokość
o boku długości 8 cm. W tym trójkącie poprowadzono wysokość 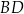 .
.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Obwód trójkąta 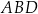 jest równy
jest równy
A) 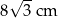 B)
B) 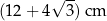 C)
C) 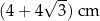 D)
D) 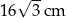
Przekątne rombu mają długości:  i
i 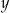 .
.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Bok tego rombu ma długość
A) 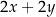 B)
B) 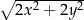 C)
C) 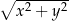 D)
D) 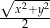
W składzie pewnego pociągu ekspresowego wagony pierwszej klasy stanowią 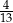 łącznej liczby wagonów pierwszej i drugiej klasy. W tym samym pociągu jest o 10 wagonów drugiej klasy więcej, niż jest wagonów pierwszej klasy. Ile łącznie wagonów pierwszej i drugiej klasy jest w tym pociągu?
łącznej liczby wagonów pierwszej i drugiej klasy. W tym samym pociągu jest o 10 wagonów drugiej klasy więcej, niż jest wagonów pierwszej klasy. Ile łącznie wagonów pierwszej i drugiej klasy jest w tym pociągu?
Sala taneczna ma kształt prostokąta o wymiarach 14 m i 12 m. Postanowiono polakierować podłogę w tej sali. Do pomalowania  powierzchni jest potrzebny jeden litr lakieru. Lakier jest sprzedawany w opakowaniach 5 litrowych po 248 zł za sztukę. Oblicz koszt zakupu lakieru potrzebnego do pomalowania podłogi tej sali.
powierzchni jest potrzebny jeden litr lakieru. Lakier jest sprzedawany w opakowaniach 5 litrowych po 248 zł za sztukę. Oblicz koszt zakupu lakieru potrzebnego do pomalowania podłogi tej sali.
W pionowym wykopie o głębokości 3,6 m umieszczono drabinę tak, że jej dolny koniec znalazł się w odległości 1,5 m od ściany wykopu. Długość drabiny jest równa 5,5 m.
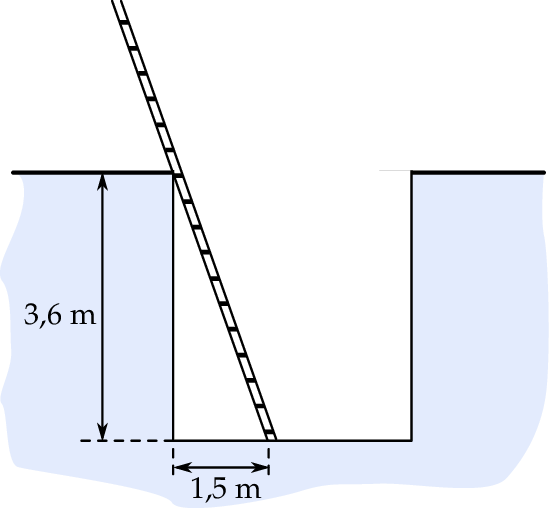
Jak jest długość części drabiny, która wystaje z wykopu powyżej powierzchni gruntu?
Punkt 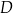 jest środkiem boku
jest środkiem boku 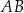 trójkąta
trójkąta 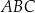 , w którym
, w którym 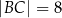 ,
, 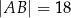 i
i 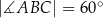 . Oblicz pole trójkąta
. Oblicz pole trójkąta 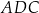 .
.

