Obwód trójkąta prostokątnego wynosi 60 cm, a tangens jednego z kątów ostrych jest równy 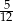 . Oblicz pole tego trójkąta oraz długość wysokości poprowadzonej z wierzchołka kąta prostego na przeciwprostokątną.
. Oblicz pole tego trójkąta oraz długość wysokości poprowadzonej z wierzchołka kąta prostego na przeciwprostokątną.
/Szkoła średnia/Geometria/Planimetria
Obwód trójkąta prostokątnego wynosi 72 cm, a tangens jednego z kątów ostrych jest równy 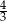 . Oblicz pole tego trójkąta oraz długość wysokości poprowadzonej z wierzchołka kąta prostego na przeciwprostokątną.
. Oblicz pole tego trójkąta oraz długość wysokości poprowadzonej z wierzchołka kąta prostego na przeciwprostokątną.
Na bokach  trójkąta równobocznego
trójkąta równobocznego 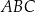 wybrano kolejno punkty
wybrano kolejno punkty  tak, że
tak, że  ,
,  i
i 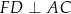 .
.

Wykaż, że trójkąt 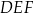 jest trójkątem równobocznym o polu trzy razy mniejszym od pola trójkąta
jest trójkątem równobocznym o polu trzy razy mniejszym od pola trójkąta 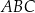 .
.
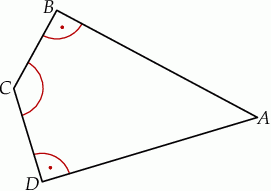
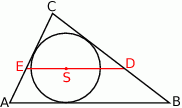
Okrąg przecina boki czworokąta 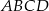 kolejno w punktach
kolejno w punktach 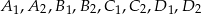 (zobacz rysunek).
(zobacz rysunek).
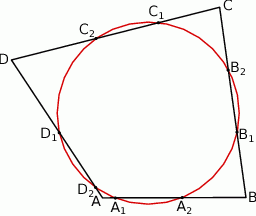
Wykaż, że jeżeli 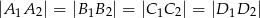 , to w czworokąt
, to w czworokąt 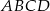 można wpisać okrąg.
można wpisać okrąg.
Dany jest trójkąt prostokątny o polu 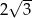 i kącie ostrym
i kącie ostrym 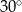 . Oblicz długości przyprostokątnych tego trójkąta.
. Oblicz długości przyprostokątnych tego trójkąta.
Dany jest trójkąt prostokątny o polu 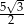 i kącie ostrym
i kącie ostrym  . Oblicz długości przyprostokątnych tego trójkąta.
. Oblicz długości przyprostokątnych tego trójkąta.
Dany jest trójkąt prostokątny o polu 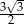 i kącie ostrym
i kącie ostrym 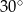 . Oblicz długości przyprostokątnych tego trójkąta.
. Oblicz długości przyprostokątnych tego trójkąta.
Liczba przekątnych wielokąta wypukłego, w którym jest  boków i
boków i 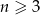 wyraża się wzorem
wyraża się wzorem 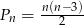 .
.
- Oblicz liczbę przekątnych w dwudziestokącie wypukłym.
- Oblicz, ile boków ma wielokąt wypukły, w którym liczba przekątnych jest pięć razy większa od liczby boków.
- Sprawdź, czy jest prawdziwe następujące stwierdzenie: Każdy wielokąt wypukły o parzystej liczbie boków ma parzystą liczbę przekątnych. Odpowiedź uzasadnij.
- Uzasadnij, że jeżeli liczba boków wielokąta wypukłego jest nieparzysta, to liczba jego przekątnych jest wielokrotnością liczby jego boków.
Kąt ostry między przekątnymi równoległoboku  ma miarę
ma miarę 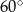 . Przekątna
. Przekątna 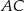 ma długość 6, a przekątna
ma długość 6, a przekątna 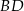 jest prostopadła do boku
jest prostopadła do boku 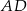 . Oblicz długości boków równoległoboku.
. Oblicz długości boków równoległoboku.
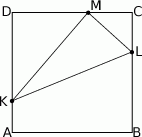
W czworokącie wypukłym 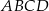 (zobacz rysunek poniżej) dane są kąty:
(zobacz rysunek poniżej) dane są kąty: 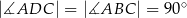 oraz
oraz 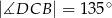 . Wykaż, że
. Wykaż, że 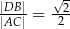 .
.
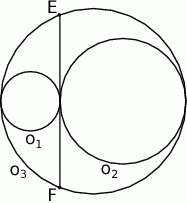
Dane są trzy okręgi 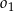 ,
, 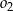 i
i 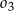 . Okręgi
. Okręgi 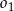 ,
, 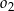 są styczne zewnętrznie, jednocześnie są styczne wewnętrznie do okręgu
są styczne zewnętrznie, jednocześnie są styczne wewnętrznie do okręgu 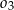 (patrz rysunek). Promienie okręgów
(patrz rysunek). Promienie okręgów 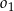 i
i 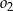 są odpowiednio równe
są odpowiednio równe 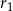 i
i 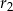 , a środki wszystkich trzech okręgów leżą na jednej prostej. Uzasadnij, że długość odcinka
, a środki wszystkich trzech okręgów leżą na jednej prostej. Uzasadnij, że długość odcinka 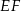 jest równa
jest równa 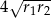 , gdzie odcinek
, gdzie odcinek 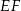 jest cięciwą okręgu
jest cięciwą okręgu 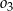 i zawiera się we wspólnej stycznej okręgów
i zawiera się we wspólnej stycznej okręgów 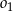 i
i  .
.
Udowodnij, że jeżeli punkt  jest środkiem ciężkości trójkąta, to
jest środkiem ciężkości trójkąta, to 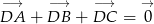 .
.
Przez środek 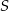 okręgu wpisanego w trójkąt
okręgu wpisanego w trójkąt 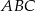 poprowadzono prostą równoległą do boku
poprowadzono prostą równoległą do boku 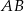 , która przecina boki
, która przecina boki 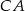 i
i 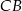 odpowiednio w punktach
odpowiednio w punktach 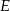 i
i 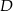 .
.
Wykaż, że 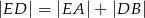 .
.
Na bokach 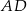 i
i 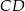 kwadratu
kwadratu  o boku długości 1 wybrano punkty
o boku długości 1 wybrano punkty 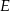 i
i 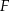 w ten sposób, że
w ten sposób, że 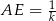 i
i 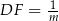 , dla
, dla 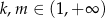 . Niech
. Niech 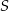 będzie punktem przecięcia odcinków
będzie punktem przecięcia odcinków 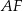 i
i 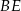
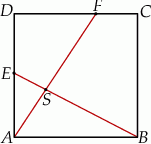
- Wykaż, że jeżeli trójkąt
 jest prostokątny to
jest prostokątny to  .
. - Oblicz cosinus kąta
 jeżeli
jeżeli 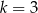 i
i 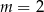 .
.
Dany jest trapez prostokątny 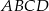 o podstawach
o podstawach 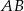 i
i 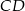 , w którym boki
, w którym boki 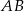 i
i 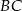 są prostopadłe. Dwusieczne kątów
są prostopadłe. Dwusieczne kątów 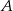 i
i 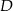 przecinają się w punkcie
przecinają się w punkcie 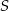 leżącym na boku
leżącym na boku 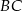 . Wykaż, że
. Wykaż, że 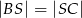 .
.
W okręgu o promieniu 5 poprowadzono dwie równoległe cięciwy o długościach 6 i 8. Oblicz odległość między tymi cięciwami.
Dany jest pięciokąt foremny 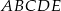 o boku długości
o boku długości  . Wiedząc, że
. Wiedząc, że 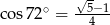
- wykaż, że długość przekątnej pięciokąta
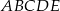 jest równa
jest równa 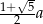 ;
; - oblicz długość promienia okręgu wpisanego w pięciokąt
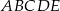 .
.
Dany jest trójkąt o wymiarach 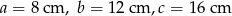 . Oblicz obwód trójkąta podobnego w skali 5.
. Oblicz obwód trójkąta podobnego w skali 5.
Dany jest trójkąt o wymiarach 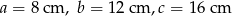 . Oblicz obwód trójkąta podobnego w skali
. Oblicz obwód trójkąta podobnego w skali 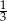 .
.
Wspólne styczne dwóch okręgów stycznych zewnętrznie przecinają się pod kątem 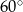 . Wyznacz stosunek długości promieni tych okręgów.
. Wyznacz stosunek długości promieni tych okręgów.
Do dwóch stycznych zewnętrznie okręgów poprowadzono dwie wspólne styczne: jedną zewnętrzną i jedną wewnętrzną. Proste te przecinają się pod kątem 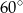 . Wyznacz stosunek długości promieni tych okręgów.
. Wyznacz stosunek długości promieni tych okręgów.
Ramię trapezu równoramiennego 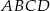 ma długość
ma długość 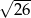 . Przekątne w tym trapezie są prostopadłe, a punkt ich przecięcia dzieli je w stosunku 2:3. Oblicz pole tego trapezu.
. Przekątne w tym trapezie są prostopadłe, a punkt ich przecięcia dzieli je w stosunku 2:3. Oblicz pole tego trapezu.
Dany jest prostokąt o polu 12, w którym długość przekątnej jest liczbą z przedziału 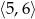 . Wykaż, że obwód tego prostokąta jest liczbą z przedziału
. Wykaż, że obwód tego prostokąta jest liczbą z przedziału 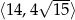 .
.
Na bokach 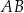 i
i 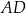 rombu
rombu 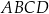 wybrano odpowiednio punkty
wybrano odpowiednio punkty 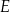 i
i 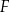 tak, że
tak, że 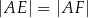 . Pole pięciokąta
. Pole pięciokąta 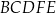 jest 17 razy większe niż pole trójkąta
jest 17 razy większe niż pole trójkąta 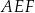 . Punkt
. Punkt 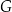 jest punktem wspólnym odcinka
jest punktem wspólnym odcinka 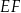 i przekątnej
i przekątnej 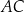 . Oblicz Oblicz
. Oblicz Oblicz 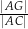 .
.
Na bokach 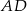 ,
, 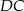 i
i 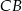 kwadratu
kwadratu 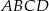 wybrano punkty
wybrano punkty 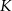 ,
, 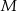 i
i 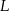 ten sposób, że
ten sposób, że 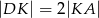 ,
, 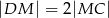 , oraz
, oraz 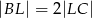 .
.
- Uzasadnij, że trójkąt
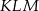 jest prostokątny.
jest prostokątny. - Oblicz tangensy kątów ostrych trójkąta
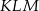 .
.