/Szkoła średnia/Zadania maturalne/Matura 2021/Matura próbna
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom rozszerzony 6 marca 2021 Czas pracy: 180 minut
Zadania zamknięte
Nieskończony malejący ciąg geometryczny 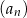 , określony dla
, określony dla 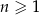 , spełnia warunki:
, spełnia warunki:
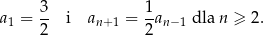
Suma wszystkich wyrazów tego ciągu jest równa
A) 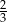 B)
B) 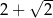 C)
C) 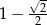 D)
D) 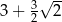
Liczba 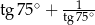 jest równa
jest równa
A) 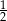 B)
B) 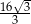 C) 4 D)
C) 4 D) 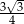
Mamy dwie urny. W pierwszej jest 5 kul białych i 5 kul czarnych, w drugiej są 3 kule białe i 7 kul czarnych. Rzucamy symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek, od jednego oczka do sześciu oczek. Jeśli w wyniku rzutu otrzymamy ściankę z liczbą oczek podzielną przez 3, to losujemy jedną kulę z pierwszej urny, w przeciwnym przypadku – losujemy jedną kulę z drugiej urny. Wtedy prawdopodobieństwo wylosowania kuli białej jest równe
A) 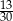 B)
B) 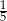 C)
C) 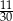 D)
D) 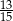
Granica 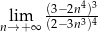 jest równa
jest równa
A) 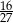 B)
B) 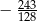 C)
C) 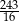 D)
D) 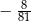
Zadania otwarte
Suma dwóch liczb jest równa 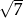 , a ich różnica jest równa
, a ich różnica jest równa 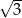 . Wykaż, że iloczyn tych liczb jest liczbą całkowitą.
. Wykaż, że iloczyn tych liczb jest liczbą całkowitą.
Wyznacz dziedzinę funkcji 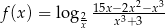
Reszta z dzielenia wielomianu 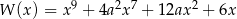 przez dwumian
przez dwumian 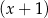 jest równa 2. Oblicz resztę z dzielenia wielomianu
jest równa 2. Oblicz resztę z dzielenia wielomianu 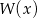 przez dwumian
przez dwumian 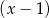 .
.
Wyznacz maksymalne przedziały monotoniczności funkcji 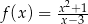 określonej dla
określonej dla 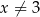 .
.
Miara kąta wewnętrznego  –kąta foremnego jest o
–kąta foremnego jest o 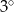 mniejsza od miary kąta wewnętrznego
mniejsza od miary kąta wewnętrznego 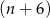 – kąta foremnego. Oblicz
– kąta foremnego. Oblicz  .
.
Dane jest równanie kwadratowe 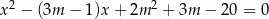 z niewiadomą
z niewiadomą  . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 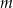 , dla których różne rozwiązania
, dla których różne rozwiązania 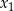 i
i 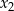 tego równania istnieją i spełniają warunek
tego równania istnieją i spełniają warunek
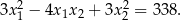
Rozwiąż równanie 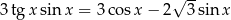 w przedziale
w przedziale 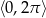 .
.
Punkt styczności okręgu o promieniu  wpisanego w trapez równoramienny dzieli ramię trapezu w stosunku 2:5. Oblicz promień okręgu opisanego na tym trapezie.
wpisanego w trapez równoramienny dzieli ramię trapezu w stosunku 2:5. Oblicz promień okręgu opisanego na tym trapezie.
W ostrosłupie prawidłowym trójkątnym krawędź boczna jest 3 razy dłuższa od krawędzi podstawy. Oblicz cosinus kąta utworzonego przez dwie sąsiednie ściany boczne.
Wierzchołki trójkąta 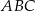 mają współrzędne:
mają współrzędne: 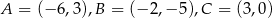 . Okrąg
. Okrąg  jest styczny do prostej
jest styczny do prostej 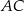 , a jego środek jest punktem przecięcia się wysokości trójkąta
, a jego środek jest punktem przecięcia się wysokości trójkąta 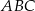 . Okrąg
. Okrąg  przecina prostą
przecina prostą 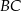 w punkcie
w punkcie 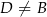 . Oblicz iloraz
. Oblicz iloraz 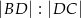 .
.
Dany jest okrąg o środku 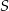 i promieniu 12. Rozpatrujemy pary okręgów: jeden o środku
i promieniu 12. Rozpatrujemy pary okręgów: jeden o środku 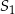 i promieniu
i promieniu  oraz drugi o środku
oraz drugi o środku 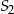 i promieniu
i promieniu 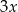 , o których wiadomo, że spełniają jednocześnie następujące warunki:
, o których wiadomo, że spełniają jednocześnie następujące warunki:
– rozważane dwa okręgi są styczne zewnętrznie;
– obydwa rozważane okręgi są styczne wewnętrznie do okręgu o środku 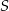 i promieniu 12;
i promieniu 12;
– punkty: 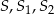 nie leżą na jednej prostej.
nie leżą na jednej prostej.
Zapisz pole trójkąta 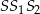 jako funkcję zmiennej
jako funkcję zmiennej  . Wyznacz dziedzinę tej funkcji i oblicz długości boków tego z rozważanych trójkątów, którego pole jest największe. Oblicz to największe pole.
. Wyznacz dziedzinę tej funkcji i oblicz długości boków tego z rozważanych trójkątów, którego pole jest największe. Oblicz to największe pole.

