/Szkoła podstawowa/Egzamin ósmoklasisty/Egzamin 2021/Próbne testy
Próbny Egzamin Ósmoklasisty
z Matematyki Zestaw przygotowany przez serwis zadania.info 24 kwietnia 2021 Czas pracy: 100 minut
W ramach prac konserwacyjnych opróżniono z wody zbiornik retencyjny. Wykres przedstawia zależność ilości pozostałej w zbiorniku wody (w 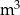 ) od czasu pracy pomp (w godzinach).
) od czasu pracy pomp (w godzinach).
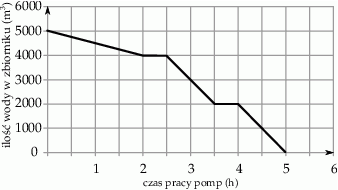
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Po 3,5 h wypompowano ze zbiornika połowę wody. | P | F |
Po 1 h wypompowano ze zbiornika 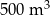 wody. wody. | P | F |
Dokończ zdanie, wybierając odpowiedź spośród podanych.
Jeżeli liczby dodatnie 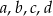 spełniają równość
spełniają równość 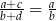 , to
, to
A) 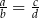 B)
B) 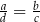 C)
C) 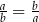 D)
D) 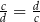
Czterech przyjaciół zarejestrowało spółkę. Wysokość udziałów poszczególnych wspólników w kapitale zakładowym spółki wyraża stosunek 12 : 8 : 3 : 2. Jaką część kapitału zakładowego stanowi udział największego inwestora?
A) 12% B) 32% C) 48% D) 52%
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Odległość na osi liczbowej między największą i najmniejszą spośród liczb: 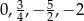 jest równa
jest równa
A) 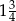 B)
B) 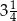 C)
C) 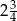 D)
D) 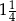
Samochód przebył trasę łączącą miejscowości 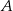 i
i 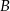 ze średnią prędkością
ze średnią prędkością 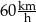 , a potem pokonał trasę między miejscowościami
, a potem pokonał trasę między miejscowościami 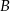 i
i 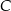 ze średnią prędkością
ze średnią prędkością 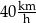 . Odległość między miastami
. Odległość między miastami 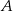 i
i 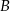 jest taka sama jak odległość między miastami
jest taka sama jak odległość między miastami 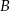 i
i 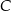 i wynosi 120 km.
i wynosi 120 km.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Średnia prędkość z jaką samochód przejechał całą trasę między 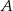 i i 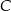 jest równa jest równa 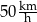 . . | P | F |
Gdyby średnia prędkość samochodu na trasie pomiędzy miastami 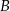 i i 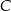 była równa była równa 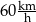 , to samochód pokonałby całą trasę między miastami , to samochód pokonałby całą trasę między miastami 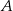 i i 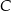 w czasie o godzinę krótszym. w czasie o godzinę krótszym. | P | F |
Dana jest liczba 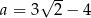 .
.
Uzupełnij poniższe zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Liczba o 2 większa od liczby  jest równa A/B .
jest równa A/B .
A) 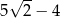 B)
B) 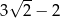
Liczba 2 razy większa od liczby  jest równa C/D .
jest równa C/D .
C) 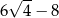 D)
D) 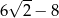
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Liczba 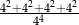 jest równa
jest równa
A) 1 B) 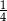 C) 4 D)
C) 4 D) 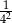
W poniższej tabeli zebrano zarobki wszystkich pracowników pewnej firmy handlowej.
| Imię pracownika | Zarobki |
| Kamila, Krzysztof, Stefan | 2800 zł |
| Zofia, Łukasz | 3000 zł |
| Ela, Marta | 3200 zł |
| Henryk | 3600 zł. |
Jaka jest średnia zarobków pracowników tej firmy? Wybierz odpowiedź spośród podanych.
A) 3050 zł B) 3150 zł C) 3200 zł D) 3250 zł
W dwóch koszach umieszczono koszulki niebieskie i czerwone. Na diagramie przedstawiono liczbę koszulek każdego koloru w I i w II koszu.
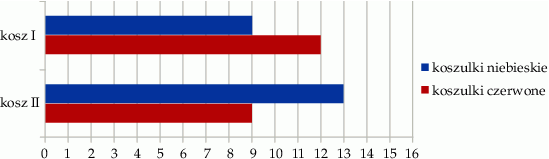
Czy wylosowanie niebieskiej koszulki z kosza I jest bardziej prawdopodobne niż wylosowanie czerwonej koszulki z kosza II? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
| Tak | Nie |
| ponieważ | |
| A) | w koszu I jest tyle samo koszulek niebieskich ile jest koszulek czerwonych w koszu II. |
| B) | stosunek liczby koszulek niebieskich do liczby koszulek czerwonych w I koszu jest taki sam jak stosunek liczby koszulek czerwonych do liczby koszulek niebieskich w II koszu. |
| C) | w koszu II jest więcej koszulek niebieskich niż jest koszulek czerwonych w pierwszym koszu. |
Ewa z sześciennych klocków o krawędzi długości 3 cm skleiła kilka brył o kształcie pokazanym na rysunku.
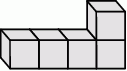
Z czterech takich brył Ewa skleiła graniastosłup prawidłowy czworokątny.
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Wysokość tego graniastosłupa jest równa A/B .
A) 12 cm B) 15 cm
Pole powierzchni bocznej utworzonego graniastosłupa jest równe C/D .
C) 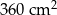 D)
D) 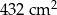
Wiadomo, że liczba 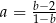 dla
dla 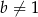 . Zatem
. Zatem
A) 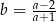 B)
B) 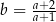 C)
C) 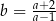 D)
D) 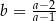
W trójkącie 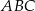 największą miarę ma kąt przy wierzchołku
największą miarę ma kąt przy wierzchołku 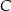 . Miara kąta przy wierzchołku
. Miara kąta przy wierzchołku 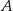 jest równa
jest równa 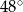 , a miara kąta przy wierzchołku
, a miara kąta przy wierzchołku 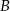 jest równa różnicy miary kąta przy wierzchołku
jest równa różnicy miary kąta przy wierzchołku 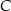 oraz miary kąta przy wierzchołku
oraz miary kąta przy wierzchołku 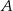 .
.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Kąt przy wierzchołku 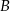 ma miarę ma miarę 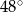 . . | P | F |
Trójkąt 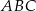 jest prostokątny. jest prostokątny. | P | F |
Marcel narysował prostokąt położony w układzie współrzędnych tak jak na pierwszym rysunku. Kolejne przystające do niego prostokąty rysował w taki sposób, że kolejny rysowany prostokąt był obrócony o 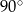 oraz lewy dolny wierzchołek tego prostokąta był prawym górnym wierzchołkiem poprzedniego prostokąta (rysunek 2.).
oraz lewy dolny wierzchołek tego prostokąta był prawym górnym wierzchołkiem poprzedniego prostokąta (rysunek 2.).
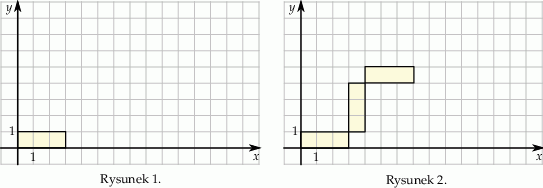
Oceń prawdziwość podanych zdań.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Jeżeli punkt
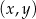 jest prawym górnym wierzchołkiem 20 prostokąta to
jest prawym górnym wierzchołkiem 20 prostokąta to 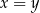 | P | F |
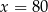 | P | F |
Odtwarzacz kosztujący 340 zł sprzedano podczas wyprzedaży za 255 zł. Obniżka wynosiła
A) 15% B) 20% C) 40% D) 25%
Obwód trójkąta 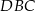 , przedstawionego na rysunku, jest równy
, przedstawionego na rysunku, jest równy
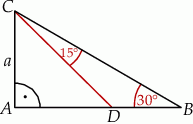
A) 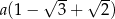 B)
B) 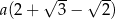 C)
C) 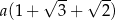 D)
D) 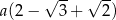
Równoległobok 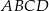 o bokach długości 6 cm i 9 cm rozcięto wzdłuż prostej
o bokach długości 6 cm i 9 cm rozcięto wzdłuż prostej  na dwa trapezy tak, jak pokazano na rysunku. Odcinek
na dwa trapezy tak, jak pokazano na rysunku. Odcinek 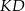 ma długość 4,8 cm.
ma długość 4,8 cm.
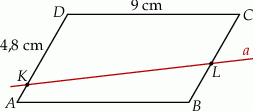
Pole trapezu 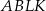 jest trzykrotnie mniejsze od pola równoległoboku
jest trzykrotnie mniejsze od pola równoległoboku 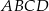 . Oblicz długość odcinka
. Oblicz długość odcinka 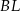 . Zapisz obliczenia.
. Zapisz obliczenia.
Uczniowie klas trzecich pewnego gimnazjum pojechali na wycieczkę pociągiem. W każdym zajętym przez nich przedziale było ośmioro uczniów. Jeśli w każdym przedziale byłoby sześcioro uczniów, to zajęliby oni o 3 przedziały więcej. Ilu uczniów pojechało na tę wycieczkę? Zapisz obliczenia.
Na rysunku przedstawiono dwie różne ściany prostopadłościanu. Jedna jest kwadratem o boku 5 cm, a druga – prostokątem o bokach 3 cm i 5 cm.
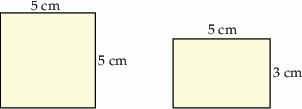
Oblicz sumę długości wszystkich krawędzi prostopadłościanu o takich wymiarach.
Na rysunku przedstawiono dwa przystające prostokąty 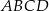 i
i 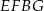 o bokach długości 5 cm i 13 cm. Oblicz długość odcinka
o bokach długości 5 cm i 13 cm. Oblicz długość odcinka 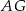 .
.