/Szkoła średnia/Zadania maturalne/Matura 2021/Matura
Egzamin Maturalny
z Matematyki (termin dodatkowy)
poziom rozszerzony 2 czerwca 2021 Czas pracy: 180 minut
Zadania zamknięte
Wartość wyrażenia 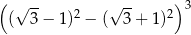 jest równa
jest równa
A) 512 B) 0 C) 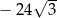 D)
D) 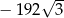
Granice 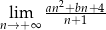 i
i 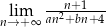 są równe. Stąd wynika, że
są równe. Stąd wynika, że
A) 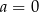 i
i 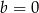 B)
B) 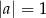 i
i 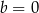 C)
C) 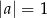 i
i 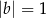 D)
D) 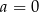 i
i 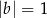
Wektory ![→ a = [m − 2,m + 2]](https://img.zadania.info/zes/0079924/HzesT13x.gif) oraz
oraz ![→ b = [m 1,5,21,5]](https://img.zadania.info/zes/0079924/HzesT14x.gif) mają równe długości wtedy i tylko wtedy, gdy
mają równe długości wtedy i tylko wtedy, gdy
A) 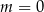 lub
lub 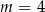 B)
B) 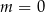 lub
lub 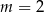 C)
C) 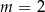 D)
D) 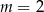 lub
lub 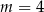
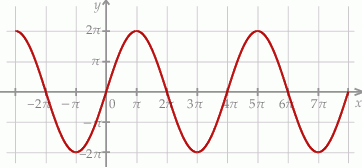
Na rysunku przedstawiono fragment wykresu pewnej funkcji  określonej dla każdej liczby rzeczywistej
określonej dla każdej liczby rzeczywistej  . Jeden z podanych poniżej wzorów jest wzorem tej funkcji. Wskaż wzór funkcji
. Jeden z podanych poniżej wzorów jest wzorem tej funkcji. Wskaż wzór funkcji  .
.
A) 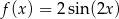 B)
B) 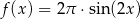
C) 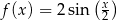 D)
D) 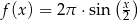
Zadania otwarte
Wynikiem dzielenia wielomianu 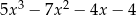 przez dwumian
przez dwumian 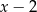 jest trójmian kwadratowy postaci
jest trójmian kwadratowy postaci 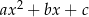 . Oblicz
. Oblicz 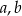 i
i  .
.
Niech 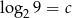 . Wykaż, że
. Wykaż, że 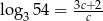 .
.
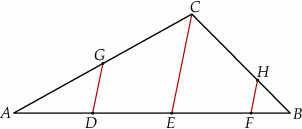
Dany jest trójkąt 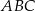 . Na boku
. Na boku 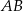 tego trójkąta obrano punkty
tego trójkąta obrano punkty 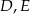 i
i 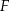 tak, że
tak, że 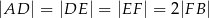 . Na bokach
. Na bokach 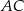 i
i 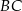 obrano – odpowiednio – punkty
obrano – odpowiednio – punkty 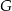 i
i 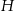 tak, że
tak, że 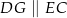 oraz
oraz 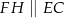 (zobacz rysunek). Wykaż, że jeżeli pole trójkąta
(zobacz rysunek). Wykaż, że jeżeli pole trójkąta 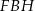 jest równe
jest równe 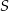 , to pole trójkąta
, to pole trójkąta 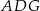 jest równe
jest równe 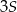 .
.
Rozwiąż równanie 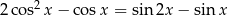 w przedziale
w przedziale 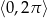 .
.
Dane są prosta 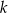 o równaniu
o równaniu 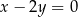 i prosta
i prosta 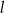 o równaniu
o równaniu 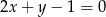 . Punkt
. Punkt  leży na prostej o równaniu
leży na prostej o równaniu 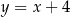 . Odległość punktu
. Odległość punktu 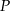 od prostej
od prostej 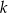 jest dwa razy większa niż odległość punktu
jest dwa razy większa niż odległość punktu 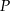 od prostej
od prostej 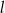 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 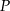 .
.
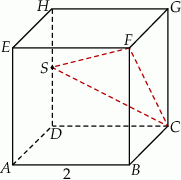
Dany jest sześcian 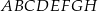 o krawędzi długości 2. Punkt
o krawędzi długości 2. Punkt 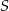 jest środkiem krawędzi
jest środkiem krawędzi 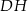 (zobacz rysunek). Oblicz miarę najmniejszego kąta wewnętrznego trójkąta
(zobacz rysunek). Oblicz miarę najmniejszego kąta wewnętrznego trójkąta 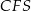 .
.
W pewnym telewizyjnym programie bierze udział trzech sportowców i pewna liczba aktorów. W trakcie tego programu uczestnicy siadają na fotelach w rzędzie, naprzeciw prowadzącego (liczba foteli jest równa liczbie uczestników). Prawdopodobieństwo zdarzenia polegającego na tym, że cała trójka sportowców będzie siedziała obok siebie przy losowym wyborze miejsc jest równe 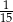 . Oblicz, ilu aktorów bierze udział w tym programie.
. Oblicz, ilu aktorów bierze udział w tym programie.
Wyznacz wszystkie wartości parametru 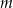 , dla których równanie
, dla których równanie
![2 2 (x− 3)[x + (m − 1)x − 6m + 2m )] = 0](https://img.zadania.info/zes/0079924/HzesT73x.gif)
ma dokładnie dwa rozwiązania.
Dana jest funkcja 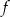 określona wzorem
określona wzorem 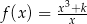 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 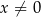 . Oblicz wartość
. Oblicz wartość 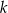 , dla której prosta o równaniu
, dla której prosta o równaniu 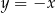 jest styczna do wykresu funkcji
jest styczna do wykresu funkcji 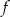 .
.
Na okręgu jest opisany czworokąt 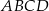 . Bok
. Bok 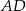 tego czworokąta jest dwa razy dłuższy od boku
tego czworokąta jest dwa razy dłuższy od boku 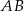 , a przekątna
, a przekątna 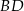 ma długość równą 6. Ponadto spełnione są następujące warunki:
ma długość równą 6. Ponadto spełnione są następujące warunki:
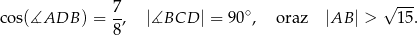
Oblicz długość boku 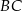 tego czworokąta.
tego czworokąta.
Rozpatrujemy wszystkie trójkąty prostokątne 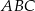 o przeciwprostokątnej
o przeciwprostokątnej 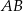 i obwodzie równym 4. Niech
i obwodzie równym 4. Niech 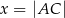 .
.
- Wykaż, że pole
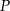 trójkąta
trójkąta 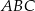 jako funkcja zmiennej
jako funkcja zmiennej  jest określone wzorem
jest określone wzorem 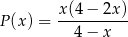
- Wyznacz dziedzinę funkcji
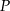 .
. - Oblicz długości boków tego z rozpatrywanych trójkątów, który ma największe pole. Oblicz to największe pole.

