Zadanie nr 1599719
Proste 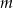 i
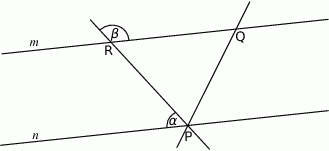
i  na poniższym rysunku są równoległe oraz
na poniższym rysunku są równoległe oraz 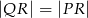 . Kąt
. Kąt 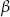 jest o
jest o 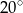 mniejszy od potrojonego kąta
mniejszy od potrojonego kąta  . Oblicz miarę
. Oblicz miarę 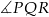 .
.
Rozwiązanie
Proste 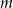 i
i  są równoległe, więc
są równoległe, więc
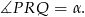
Stąd
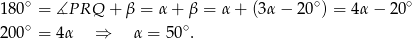
Miarę kąta 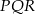 obliczamy korzystające z tego, że suma kątów w trójkącie równoramiennym
obliczamy korzystające z tego, że suma kątów w trójkącie równoramiennym 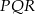 jest równa
jest równa 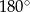 . Mamy zatem
. Mamy zatem
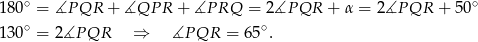
Odpowiedź: