/Szkoła średnia/Prawdopodobieństwo/Z definicji

Zadanie nr 5551518

Dodaj do ulubionych
Dodaj do rozwiązanych

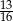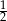W urnie znajdują się drewniane klocki, przy czym każdy z klocków jest biały lub czarny oraz każdy z klocków ma kształt kuli lub sześcianu. Wiadomo, że prawdopodobieństwo wylosowania czarnego klocka jest równe 1316- , prawdopodobieństwo wylosowania klocka w kształcie sześcianu jest równe 5 8 , a prawdopodobieństwo wylosowania klocka, który jest biały lub jest kulą jest równe 1 2 . Oblicz prawdopodobieństwo wybrania klocka, który jest białą kulą.

Rozwiązanie

Będziemy korzystać ze wzoru na prawdopodobieństwo sumy

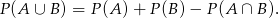
P(A ∪ B) = P (A )+ P (B) − P (A ∩ B ).

Jeżeli przyjmiemy, że 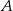A oznacza zdarzenie polegające na wylosowaniu białego klocka, a 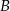B zdarzenie polegające na wybraniu kuli, to musimy obliczyć 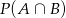P (A ∩ B ) . Mamy natomiast podane

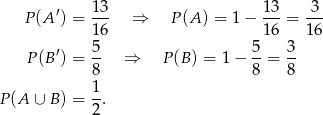
′ 1-3 13- 3-- P (A ) = 1 6 ⇒ P (A) = 1− 16 = 16 5 5 3 P (B′) = -- ⇒ P(B ) = 1 − --= -- 8 8 8 P(A ∪ B) = 1-. 2

Stąd

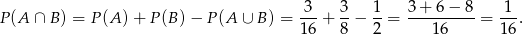
3 3 1 3 + 6 − 8 1 P (A ∩ B ) = P(A )+ P(B )− P(A ∪ B ) = ---+ --− --= ----------= --. 16 8 2 16 16

 
Odpowiedź: -1 16

Wersja PDF