W czworokącie 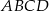 przekątne przecinają się w punkcie o współrzędnych
przekątne przecinają się w punkcie o współrzędnych 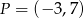 w taki sposób, że
w taki sposób, że 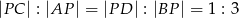 . Wiedząc, że
. Wiedząc, że ![− → AC = [4,6]](https://img.zadania.info/zad/3335440/HzadT3x.gif) i
i ![−→ BD = [− 10,− 2]](https://img.zadania.info/zad/3335440/HzadT4x.gif) , oblicz współrzędne wierzchołków tego czworokąta. Uzasadnij, że czworokąt
, oblicz współrzędne wierzchołków tego czworokąta. Uzasadnij, że czworokąt 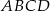 jest trapezem.
jest trapezem.
/Szkoła średnia/Geometria/Geometria analityczna/Wektory/Czworokąt
W prostokącie 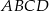 dane są wierzchołek
dane są wierzchołek 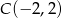 i wektor
i wektor ![→ AB = [3 ,3]](https://img.zadania.info/zad/3365079/HzadT2x.gif) . Wyznacz równania prostych, zawierających przekątne tego prostokąta, jeśli wiadomo, że wierzchołek
. Wyznacz równania prostych, zawierających przekątne tego prostokąta, jeśli wiadomo, że wierzchołek 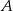 należy do prostej o równaniu
należy do prostej o równaniu 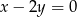 .
.
W prostokącie 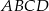 dany jest wierzchołek
dany jest wierzchołek 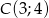 oraz
oraz ![−→ AB = [4;3]](https://img.zadania.info/zad/4338487/HzadT2x.gif) . Znajdź równania przekątnych wiedząc, że wierzchołek
. Znajdź równania przekątnych wiedząc, że wierzchołek 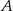 należy do prostej
należy do prostej 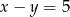 .
.
Za pomocą rachunku wektorowego pokazać, że środki boków dowolnego czworokąta tworzą wierzchołki równoległoboku.
Punkt 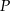 jest punktem wspólnym przekątnych trapezu
jest punktem wspólnym przekątnych trapezu 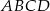 , w którym
, w którym 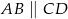 oraz
oraz ![−→ −→ −→ D = (1 0,− 9),AB = [12,21],CB = [0,13],CP = [− 3,− 2]](https://img.zadania.info/zad/6347587/HzadT3x.gif) . Oblicz współrzędne pozostałych wierzchołków trapezu
. Oblicz współrzędne pozostałych wierzchołków trapezu 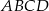 .
.
Punkt 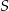 jest punktem przecięcia się przekątnych równoległoboku
jest punktem przecięcia się przekątnych równoległoboku 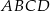 , a punkt
, a punkt 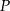 jest takim punktem boku
jest takim punktem boku 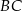 tego równoległoboku, że
tego równoległoboku, że 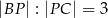 . Oblicz współrzędne spodka wysokości opuszczonej z wierzchołka
. Oblicz współrzędne spodka wysokości opuszczonej z wierzchołka 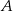 tego równoległoboku na prostą
tego równoległoboku na prostą 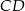 , jeżeli
, jeżeli ![−→ AB = [4,4]](https://img.zadania.info/zad/7923031/HzadT7x.gif) ,
, ![−→ DS = [3,− 3]](https://img.zadania.info/zad/7923031/HzadT8x.gif) i
i 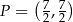 .
.
W kartezjańskim układzie współrzędnych 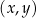 czworokąt
czworokąt 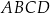 jest równoległobokiem takim, że
jest równoległobokiem takim, że ![−→ BD = [− 21,− 7]](https://img.zadania.info/zad/8179651/HzadT2x.png) i
i ![−→ DC = [15,8 ]](https://img.zadania.info/zad/8179651/HzadT3x.png) . Oblicz pole tego równoległoboku.
. Oblicz pole tego równoległoboku.
W czworokącie 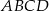 dane są
dane są ![−→ −→ AB = [6,− 3], DA = [− 8,− 7]](https://img.zadania.info/zad/8185465/HzadT1x.gif) oraz środek
oraz środek 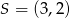 przekątnej
przekątnej 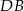 . Wyznacz współrzędne rzutu prostopadłego punktu
. Wyznacz współrzędne rzutu prostopadłego punktu 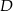 na prostą
na prostą 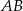 .
.
Punkt 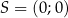 jest środkiem boku
jest środkiem boku 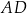 równoległoboku
równoległoboku 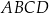 . Wiadomo też, że
. Wiadomo też, że ![−→ AB = [4;3]](https://img.zadania.info/zad/9290117/HzadT3x.png) oraz
oraz ![−→ BC = [6;2]](https://img.zadania.info/zad/9290117/HzadT4x.png) . Wyznacz wierzchołki tego równoległoboku.
. Wyznacz wierzchołki tego równoległoboku.

