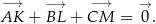Udowodnij, że jeżeli punkt 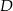 jest środkiem ciężkości trójkąta, to
jest środkiem ciężkości trójkąta, to 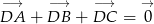 .
.
/Szkoła średnia/Geometria/Geometria analityczna/Wektory/Trójkąt
Na bokach 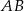 i
i 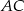 trójkąta
trójkąta 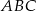 wybrano punkty
wybrano punkty 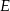 i
i 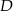 w ten sposób, że
w ten sposób, że 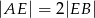 i
i 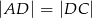 . Punkt
. Punkt 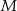 jest punktem wspólnym odcinków
jest punktem wspólnym odcinków 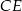 i
i 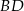 .
.
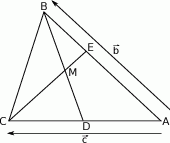
- Przedstaw każdy z wektorów
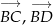 oraz
oraz 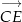 w postaci
w postaci 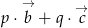 , gdzie
, gdzie 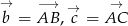 oraz
oraz 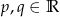 .
. - Korzystając z równości
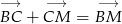 oblicz w jakim stosunku punkt
oblicz w jakim stosunku punkt 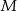 dzieli odcinki
dzieli odcinki 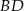 i
i 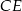 .
.
W trójkącie 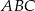 dane są
dane są 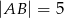 ,
, 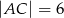 oraz iloczyn skalarny
oraz iloczyn skalarny 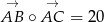 . Oblicz miarę kąta
. Oblicz miarę kąta 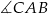 oraz pole tego trójkąta.
oraz pole tego trójkąta.
W trójkącie 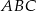 dane są
dane są 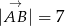 ,
, 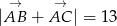 oraz
oraz 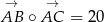 . Oblicz długość boku
. Oblicz długość boku 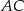 , oraz miarę kąta
, oraz miarę kąta 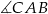 .
.
Trójkąt jest rozpięty na wektorach 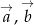 . Wyrazić środkowe tego trójkąta przez wektory
. Wyrazić środkowe tego trójkąta przez wektory 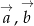 .
.
Dane są wektory ![→ a = [1,− 2]](https://img.zadania.info/zad/8690556/HzadT0x.gif) ,
, ![→ b = [− 2,− 1]](https://img.zadania.info/zad/8690556/HzadT1x.gif) ,
, ![→ c = [3,4]](https://img.zadania.info/zad/8690556/HzadT2x.gif) . Dobierz wartości parametrów
. Dobierz wartości parametrów 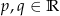 tak, aby wektory
tak, aby wektory 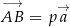 ,
, 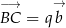 i
i 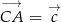 tworzyły trójkąt
tworzyły trójkąt 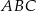 .
.
Punkty 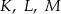 są środkami boków
są środkami boków 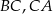 i
i 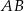 trójkąta
trójkąta 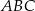 . Wykaż, że
. Wykaż, że