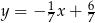Zadanie nr 4338487
W prostokącie 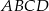 dany jest wierzchołek
dany jest wierzchołek 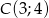 oraz
oraz ![−→ AB = [4;3]](https://img.zadania.info/zad/4338487/HzadT2x.gif) . Znajdź równania przekątnych wiedząc, że wierzchołek
. Znajdź równania przekątnych wiedząc, że wierzchołek 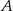 należy do prostej
należy do prostej 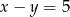 .
.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
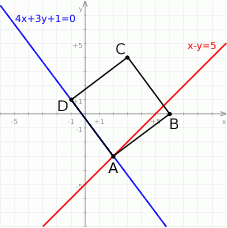
Ponieważ 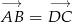 możemy łatwo wyliczyć współrzędne wierzchołka
możemy łatwo wyliczyć współrzędne wierzchołka 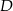 .
.
![−→ DC = [4 ,3] = C − D = [3− xD ,4 − yD ] { 4 = 3− xD ⇒ xD = − 1 3 = 4− yD ⇒ yD = 1 .](https://img.zadania.info/zad/4338487/HzadR3x.gif)
Zatem 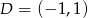 . Mając współrzędne punkt
. Mając współrzędne punkt 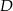 możemy teraz napisać równanie prostej
możemy teraz napisać równanie prostej 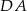 (jest prostopadła do
(jest prostopadła do 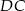 ) i przechodzi przez
) i przechodzi przez 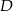 . To z kolei pozwoli wyznaczyć współrzędne punktu
. To z kolei pozwoli wyznaczyć współrzędne punktu 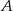 (bo wiemy, że leży on też na prostej
(bo wiemy, że leży on też na prostej 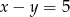 ). Równanie prostej
). Równanie prostej 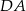 napiszemy korzystając ze wzoru na równanie prostej prostopadłej do wektora
napiszemy korzystając ze wzoru na równanie prostej prostopadłej do wektora ![→v = [p,q]](https://img.zadania.info/zad/4338487/HzadR12x.gif) i przechodzącej przez punkt
i przechodzącej przez punkt 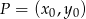
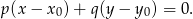
W naszej sytuacji mamy ![→ −→ v = AB = [4,3]](https://img.zadania.info/zad/4338487/HzadR15x.gif) i
i 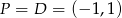 . Prosta
. Prosta 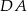 ma więc równanie
ma więc równanie
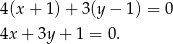
Szukamy teraz punktu wspólnego tej prostej z daną prostą 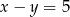 . Podstawiamy
. Podstawiamy 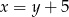 do powyższego równania.
do powyższego równania.
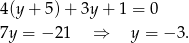
Stąd 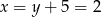 i
i 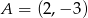 . Teraz już łatwo obliczyć współrzędne wierzchołka
. Teraz już łatwo obliczyć współrzędne wierzchołka 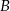 .
.
![−→ [4,3] = AB = B − A = [xB − 2,yB + 3].](https://img.zadania.info/zad/4338487/HzadR25x.gif)
Stąd 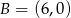 .
.
Pozostało napisać równania prostych 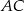 i
i 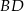 . Korzystamy ze wzoru na równanie prostej przechodzącej przez dwa punkty
. Korzystamy ze wzoru na równanie prostej przechodzącej przez dwa punkty 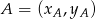 i
i 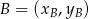 :
:
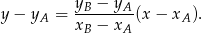
Najpierw prosta 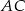
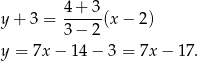
Teraz prosta 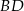
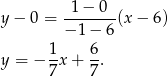
Odpowiedź: 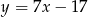 i
i