/Szkoła średnia/Statystyka

Zadanie nr 3618414

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest skończony ciąg arytmetyczny o 2018 wyrazach. Wykaż, że średnia arytmetyczna i mediana wszystkich wyrazów tego ciągu są równe.

Rozwiązanie

Jeżeli oznaczymy dany ciąg przez 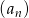(an) , to średnia arytmetyczna jego wyrazów jest równa (korzystamy ze wzoru na sumę kolejnych wyrazów ciągu arytmetycznego)

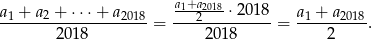
a+a a1 +-a2 +-⋅⋅-⋅+-a2018 -1-22018-⋅2018- a1-+-a2018 2 018 = 2018 = 2 .

Aby obliczyć medianę rozważmy dwa przypadki. Jeżeli dany ciąg jest stały (tzn. wszystkie wyrazy są takie same), to oczywiście mediana jest równa 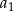a 1 i jest równa średniej:

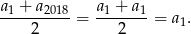
a1 + a2018 a1 + a1 ----------= ------- = a 1. 2 2

Jeżeli natomiast ciąg nie jest stały, to jest rosnący lub malejący i mediana to średnia arytmetyczna dwóch środkowych wyrazów tego ciągu, czyli jest równa

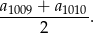
a + a -1009----1010. 2

Wystarczy zatem wykazać, że

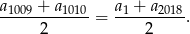
a1009 +-a1010- a1 +-a2018- 2 = 2 .

Zrobimy to na dwa sposoby.

Sposób I

Korzystamy ze wzoru na n -ty wyraz ciągu arytmetycznego.

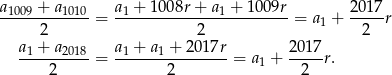
a1009 +-a1010-= a1-+-1008r-+-a1-+-1009r-= a + 2017-r 2 2 1 2 a1 + a2018 a1 + a1 + 2017r 2017 ----------= ----------------= a1 + -----r. 2 2 2

Sposób II

Zauważmy, że

a1-+-a2018= a1-+-a1-+-2017r-= a1-+-1008r-+-a1-+-100-9r= a1009 +-a1010-. 2 2 2 2
Wersja PDF