Prostokąt/Czworokąt/Planimetria - zadania z matematyki

/Szkoła średnia/Geometria/Planimetria/Czworokąt/Prostokąt

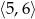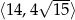Dany jest prostokąt o polu 12, w którym długość przekątnej jest liczbą z przedziału ⟨5,6⟩ . Wykaż, że obwód tego prostokąta jest liczbą z przedziału √ --- ⟨14 ,4 15⟩ .

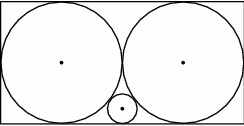
W prostokąt wpisano trzy parami styczne okręgi w ten sposób, że dwa z nich są styczne do trzech boków, prostokąta, a trzeci jest styczny do jednego z boków prostokąta (patrz rysunek). Oblicz promień mniejszego okręgu jeżeli promień większego okręgu jest równy .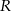

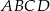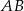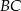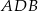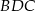W prostokącie ABCD , w którym stosunek długości boków i jest równy 4:3, poprowadzono dwusieczne kątów ADB i BDC . Dwusieczne te przecinają bok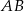i i 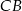odpowiednio w punktach 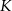i 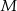. Oblicz stosunek pola prostokąta 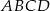ABCD do pola trójkąta DKM .

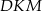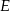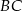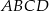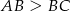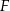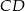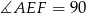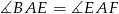Punkt jest środkiem boku prostokąta ABCD , w którym AB > BC . Punkt leży na boku tego prostokąta oraz ∡AEF = 90 . Udowodnij, że ∡BAE = ∡EAF .

Dany jest prostokąt o polu 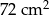2 72 cm . Gdyby zwiększyć długość jednego z boków o 2 cm, a drugi bok zmniejszyć o 3 cm, to pole nie ulegnie zmianie. Oblicz długości boków danego prostokąta.

Ukryj Podobne zadania

Dany jest prostokąt o polu 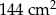2 1 44 cm . Gdyby zwiększyć długość jednego z boków o 8 cm, a drugi bok zmniejszyć o 3 cm, to pole nie ulegnie zmianie. Oblicz długości boków danego prostokąta.

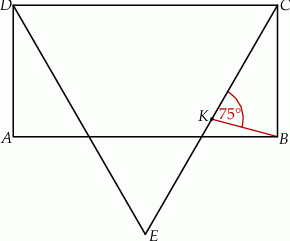
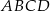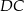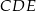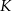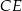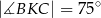Dany jest prostokąt ABCD , którego jeden bok jest dwa razy dłuższy od drugiego. Na boku zbudowano trójkąt równoboczny CDE (zobacz rysunek). Punkt jest takim punktem odcinka , że |∡BKC | = 7 5∘ . Udowodnij, że punkt 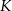jest środkiem odcinka .

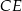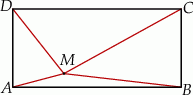
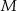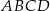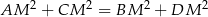Punkt leży wewnątrz prostokąta ABCD (zob. rysunek). Udowodnij, że AM 2 + CM 2 = BM 2 + DM 2 .

W trójkącie równoramiennym dane są długości podstawy 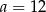a = 12 cm i wysokości 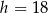h = 18 cm. W trójkąt ten wpisano prostokąt w ten sposób, że dwa wierzchołki prostokąta leżą na podstawie, a po jednym na każdym ramieniu trójkąta, przy czym przekątne prostokąta są równoległe do ramion trójkąta. Oblicz długości boków prostokąta.

Dany jest prostokąt 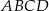ABCD , którego boki mają długości i 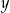. Punkt 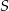jest punktem przecięcia się przekątnych prostokąta.

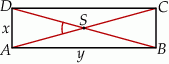
Wykaż, że pole trójkąta 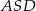jest cztery razy mniejsze od pola prostokąta .
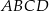Wiedząc dodatkowo, że 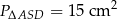i 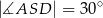, oblicz pole kwadratu, którego bok ma długość .

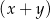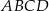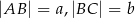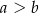Dany jest prostokąt ABCD , w którym |AB | = a,|BC | = b i a > b . Odcinek 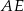jest wysokością trójkąta 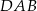DAB opuszczoną na jego bok 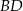. Wyraź pole trójkąta 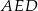AED za pomocą i .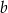

Dwa przeciwległe boki kwadratu wydłużono dwukrotnie, a każdy z dwóch pozostałych skrócono o 3 cm. Pole otrzymanego prostokąta jest o 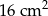1 6 cm 2 większe od pola kwadratu. Oblicz długości boków prostokąta.

Ukryj Podobne zadania

Dwa przeciwległe boki kwadratu wydłużono trzykrotnie, a każdy z dwóch pozostałych wydłużono o 2 cm. Pole otrzymanego prostokąta jest o 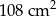108 cm 2 większe od pola kwadratu. Oblicz długości boków prostokąta.

W prostokącie 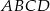ABCD , w którym 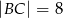|BC | = 8 połączono wierzchołek 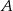z punktem 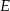leżącym na boku 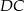. Odcinek ten przeciął przekątną 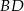w punkcie .

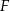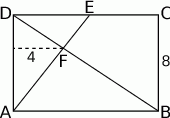
Wiedząc, że odległość punktu 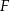od boku 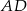jest równa 4, oraz że 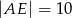|AE | = 10 oblicz długość boku 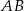prostokąta.

W prostokącie, którego krótszy bok ma długość 8 zawarty jest kwadrat o boku równym różnicy

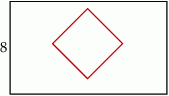
długości boków prostokąta, i którego przekątne są równoległe do boków prostokąta.

Wyraź pole pozostałe po wycięciu kwadratu z prostokąta jako funkcję dłuższego boku prostokąta. Wyznacz dziedzinę otrzymanej funkcji.
Wykaż, że różnica pól prostokąta i kwadratu jest zawsze większa od 64.

W trójkąt równoramienny, którego ramię jest równe 5 cm, a podstawa równa się 6 cm, wpisano prostokąt w ten sposób, że dwa jego wierzchołki leżą na podstawie, a pozostałe leżą na ramionach trójkąta. Wyznacz obwód i pole prostokąta jako funkcję jego wysokości.

Obwód prostokąta wynosi 60 cm. Jeśli krótszy bok tego prostokąta zwiększymy o 3 cm, a dłuższy skrócimy o 3 cm, to otrzymamy kwadrat. Wyznacz kąt pomiędzy przekątną, a dłuższym bokiem prostokąta. Wynik podaj z dokładnością do .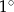

Ukryj Podobne zadania

Obwód prostokąta wynosi 32 cm. Jeśli krótszy bok tego prostokąta zwiększymy o 3 cm, a dłuższy skrócimy o 3 cm, to otrzymamy kwadrat. Wyznacz kąt pomiędzy przekątną, a dłuższym bokiem prostokąta. Wynik podaj z dokładnością do .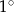

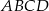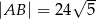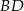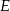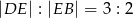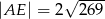Dany jest prostokąt ABCD , w którym √ -- |AB | = 24 5 . Na przekątnej leży punkt taki, że |DE | : |EB | = 3 : 2 oraz √ ---- |AE | = 2 2 69 . Oblicz pole prostokąta ABCD .

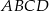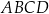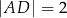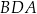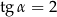Dany jest prostokąt ABCD , w którym |AD | = 2 . Kąt BDA ma miarę , taką, że tgα = 2 . Przekątna 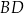i prosta przechodząca przez wierzchołek 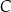prostopadła do 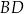przecinają się w punkcie 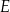(zobacz rysunek).

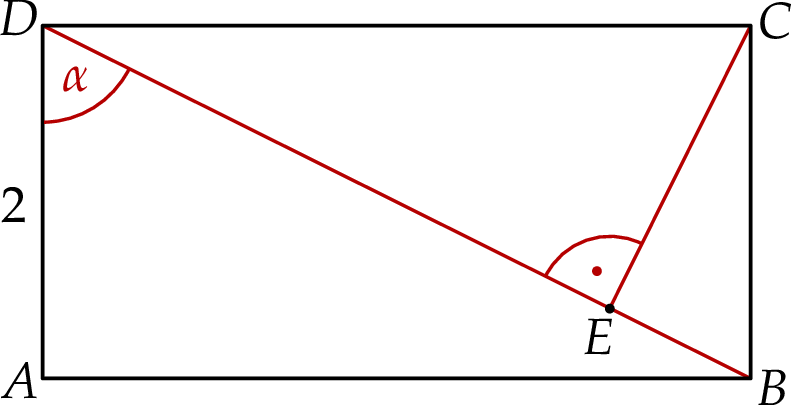
ZINFO-FIGURE

Oblicz długość odcinka .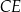

Z przeciwległych wierzchołków prostokąta poprowadzono odcinki prostopadłe do przekątnej. Odcinki te dzielą przekątną na trzy części. Każda z nich jest odcinkiem o długości 4 cm. Oblicz pole tego prostokąta.

Dany jest prostokąt 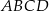ABCD , w którym 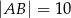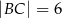|AB | = 10 , |BC | = 6 . Odcinek 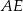jest wysokością trójkąta 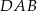DAB opuszczoną na jego bok 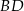. Oblicz pole trójkąta AED .

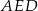Punkty 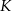i 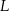dzielą podstawę 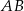trapezu 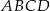ABCD na trzy równe części, a punkty 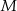i 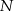dzielą podstawę 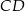tego trapezu na trzy równe części. Pole czworokąta 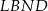LBND jest równe 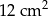12 cm 2 . Oblicz pole trapezu ABCD .

Strona 1 z 3