Oblicz jaka może być najmniejsza możliwa długość boku 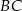 trójkąta
trójkąta 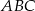 jeżeli
jeżeli 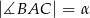 i pole trójkąta
i pole trójkąta 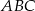 jest równe
jest równe 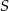 .
.
/Konkursy/Zadania/Geometria/Planimetria/Trójkąt
Środkowa trójkąta jest równa połowie boku, do którego została poprowadzona. Wykaż, że trójkąt ten jest prostokątny.
W trójkacie 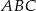 dwusieczna kąta
dwusieczna kąta 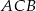 przecina bok
przecina bok 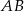 w punkcie
w punkcie 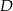 . Długosci boków
. Długosci boków 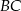 i
i 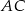 są równe odpowiednio
są równe odpowiednio  i
i 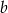 , a długość odcinka
, a długość odcinka 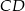 jest równa
jest równa 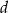 . Wykaż, że
. Wykaż, że 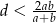 .
.
W trójkąt równoboczny o boku długości 6 cm wpisano kwadrat. Oblicz pole tego kwadratu.
Znaleźć pole kwadratu wpisanego w trójkąt równoboczny o boku 4 cm.
Na boku 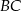 trójkąta
trójkąta 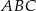 wybrano punkt
wybrano punkt 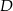 tak, by
tak, by 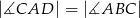 . Odcinek
. Odcinek 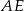 jest dwusieczną kąta
jest dwusieczną kąta 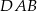 . Udowodnij, że
. Udowodnij, że 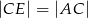 .
.
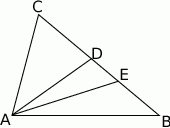
W trójkącie 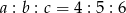 . Wykaż, że w tym trójkącie
. Wykaż, że w tym trójkącie 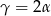 .
.
Boki trójkąta 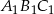 są styczne do okręgu w punktach
są styczne do okręgu w punktach 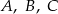 , a kąty trójkąta
, a kąty trójkąta 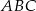 są odpowiednio równe
są odpowiednio równe 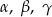 . Oblicz miary kątów trójkąta
. Oblicz miary kątów trójkąta 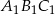 .
.
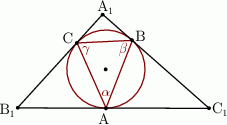
Wykaż, że jeżeli kąty wewnętrzne trójkąta spełniają warunek 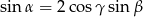 to trójkąt ten jest równoramienny.
to trójkąt ten jest równoramienny.
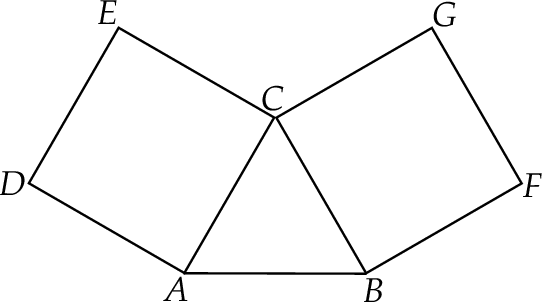
Wysokość trójkąta prostokątnego poprowadzona do przeciwprostokątnej ma długość 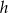 i jest pięć razy krótsza od obwodu tego trójkąta. Oblicz długości boków trójkąta.
i jest pięć razy krótsza od obwodu tego trójkąta. Oblicz długości boków trójkąta.
Na bokach trójkąta równobocznego zbudowano dwa kwadraty w sposób pokazany na rysunku.
Wykaż, że punkty 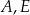 i
i 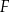 są wierzchołkami trójkąta prostokątnego.
są wierzchołkami trójkąta prostokątnego.
Na bokach 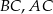 i
i 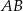 trójkąta
trójkąta 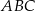 wybrano odpowiednio punkty
wybrano odpowiednio punkty 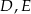 i
i 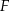 . Wykaż, że jeżeli okręgi opisane na trójkątach
. Wykaż, że jeżeli okręgi opisane na trójkątach 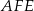 i
i 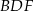 są styczne, to punkt
są styczne, to punkt 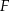 leży na okręgu opisanym na trójkącie
leży na okręgu opisanym na trójkącie 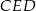 .
.
Znaleźć pole kwadratu wpisanego w trójkąt równoboczny o boku 4. Jakie pole ma koło opisane na tym kwadracie?
W trójkącie równoramiennym (patrz rysunek) długość podstawy wynosi  , zaś wysokości opuszczone odpowiednio na podstawę i ramię są równe
, zaś wysokości opuszczone odpowiednio na podstawę i ramię są równe 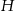 i
i 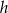 . Kąt między ramieniem trójkąta i wysokością opuszczoną na podstawę ma miarę
. Kąt między ramieniem trójkąta i wysokością opuszczoną na podstawę ma miarę  .
.
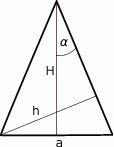
- Wyraź
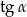 w zależności od wielkości
w zależności od wielkości  i
i 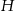 .
. - Wyraź
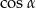 w zależności od wielkości
w zależności od wielkości  i
i 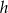 .
. - Wykaż, że jeśli
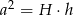 , to
, to 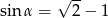 .
.
Oblicz miary kątów trójkąta, w którym długości boków tworzą ciąg geometryczny, a miary kątów tworzą ciąg arytmetyczny.
W trójkącie 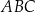 kąt
kąt 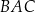 jest dwa razy większy od kąta
jest dwa razy większy od kąta 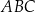 . Wykaż, że prawdziwa jest równość
. Wykaż, że prawdziwa jest równość 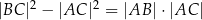 .
.
Dany jest trójkąt 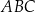 , który nie jest równoramienny. W tym trójkącie miara kąta
, który nie jest równoramienny. W tym trójkącie miara kąta 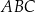 jest dwa razy większa od miary kąta
jest dwa razy większa od miary kąta 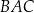 . Wykaż, że długości boków tego trójkąta spełniają warunek
. Wykaż, że długości boków tego trójkąta spełniają warunek
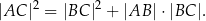
Okrąg wpisany w trójkąt 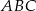 jest styczny do boków
jest styczny do boków 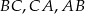 odpowiednio w punktach
odpowiednio w punktach 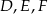 . Punkty
. Punkty 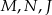 są odpo- wiednio środkami okręgów wpisanych w trójkąty
są odpo- wiednio środkami okręgów wpisanych w trójkąty 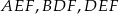 . Dowieść, że punkty
. Dowieść, że punkty 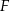 i
i 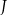 są symetryczne względem prostej
są symetryczne względem prostej 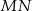 .
.

