/Konkursy/Zadania/Geometria/Planimetria/Trójkąt

Zadanie nr 2790118

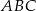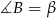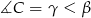W okrąg wpisany jest trójkąt ABC , przy czym ∡B = β i ∡C = γ < β . Oblicz miarę kąta między prostą 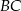BC i styczną do okręgu w punkcie A .

Wersja PDF

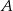Rozwiązanie

Na mocy twierdzenia o stycznej i siecznej 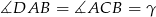∡DAB = ∡ACB = γ .

PIC

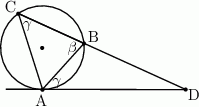
Ponadto

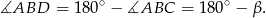
∡ABD = 180∘ − ∡ABC = 180∘ − β .

Suma kątów w trójkącie 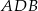ADB jest równa 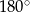1 80∘ , więc

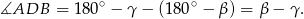
∡ADB = 18 0∘ − γ− (180∘ − β) = β− γ.

 
Odpowiedź: β − γ

Wersja PDF