Zadanie nr 3107027
Udowodnij że jeśli dwie dwusieczne w trójkącie są sobie równe to trójkąt jest równoramienny (twierdzenie Steinera-Lehmusa).
Rozwiązanie
Sposób I
Zaczniemy od wyprowadzenia wzoru na długość 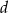 dwusiecznej poprowadzonej do boku długości
dwusiecznej poprowadzonej do boku długości 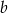 w trójkącie o bokach
w trójkącie o bokach 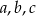 .
.

Z twierdzeń cosinusów w trójkątach 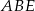 i
i 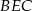 mamy
mamy

Aby pozbyć 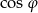 mnożymy pierwsze równanie przez
mnożymy pierwsze równanie przez 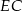 a drugie przez
a drugie przez 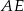 i dodajemy stronami.
i dodajemy stronami.
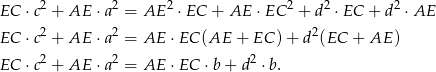
Równość, którą otrzymaliśmy, to tak zwane twierdzenie Stewarta – zauważmy, że jak dotąd nie korzystaliśmy z tego, że 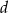 jest dwusieczną.
jest dwusieczną.
Odcinki 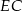 i
i 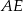 możemy wyliczyć z twierdzenia o dwusiecznej.
możemy wyliczyć z twierdzenia o dwusiecznej.
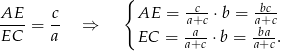
Mamy więc

Aby otrzymać długość  dwusiecznej poprowadzonej z wierzchołka
dwusiecznej poprowadzonej z wierzchołka 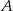 musimy w tym wzorze zamienić
musimy w tym wzorze zamienić  z
z 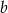 , czyli
, czyli
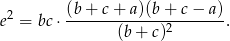
Równość dwusiecznych daje nam równanie:

Teraz wystarczy zauważyć, że 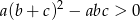 , więc wyrażenie w drugim nawiasie jest dodatnie, czyli
, więc wyrażenie w drugim nawiasie jest dodatnie, czyli 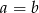 .
.
Sposób II
Tym razem pozostaniemy w świecie geometrii i udowodnimy ogólniejszy fakt, że jeżeli  to długości dwusiecznych
to długości dwusiecznych 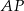 i
i 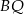 spełniają
spełniają 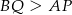 . Oczywiście wynika z tego nasze zadanie.
. Oczywiście wynika z tego nasze zadanie.
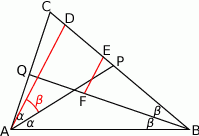
Oznaczmy 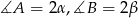 . Ponieważ
. Ponieważ  , na odcinku
, na odcinku 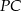 istnieje punkt
istnieje punkt 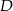 spełniający
spełniający 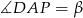 . W trójkącie
. W trójkącie  mamy
mamy 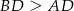 (na przeciw większego kąta leży większy bok), zatem na odcinku
(na przeciw większego kąta leży większy bok), zatem na odcinku 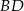 istnieje punkt
istnieje punkt 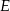 taki, że
taki, że 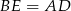 . Teraz wybierzmy punkt
. Teraz wybierzmy punkt 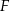 na
na  tak, aby odcinki
tak, aby odcinki 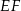 i
i 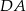 były równoległe.
były równoległe.
Trójkąty  i
i  mają dwa równe kąty i równe odpowiadające boki
mają dwa równe kąty i równe odpowiadające boki 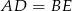 . Są więc przystające. Zatem
. Są więc przystające. Zatem  , co kończy dowód.
, co kończy dowód.
Dowód ten, (według Coxetra) pochodzi od H.G. Fordera.
Sposób III
Kolejny geometryczny dowód (W. T. Williams & G. H. Savage).
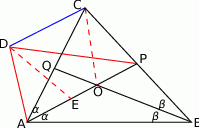
Załóżmy, że 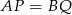 i zbudujmy na dwusiecznej
i zbudujmy na dwusiecznej 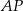 trójkąt
trójkąt 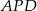 przystający do trójkąta
przystający do trójkąta 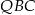 .
.
Niech 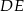 będzie dwusieczną kąta
będzie dwusieczną kąta 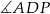 . Odcinek jest więc równy odpowiadającemu fragmentowi
. Odcinek jest więc równy odpowiadającemu fragmentowi 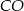 dwusiecznej w trójkącie
dwusiecznej w trójkącie 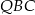 .
.
Ponieważ 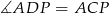 , na czworokącie
, na czworokącie 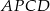 można opisać okrąg. Pokażemy, że okrąg można również opisać na czworokącie
można opisać okrąg. Pokażemy, że okrąg można również opisać na czworokącie  :
:
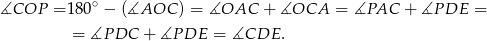
Zatem 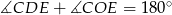 i rzeczywiście na czworokącie
i rzeczywiście na czworokącie 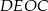 można opisać okrąg. Wcześniej zauważyliśmy, że
można opisać okrąg. Wcześniej zauważyliśmy, że 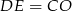 , więc jest to trapez równoramienny i odcinki
, więc jest to trapez równoramienny i odcinki 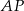 i
i 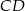 są do siebie równoległe. To jednak oznacza, że
są do siebie równoległe. To jednak oznacza, że
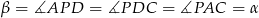
co kończy dowód.
Sposób IV
Tym razem dowód pochodzący od W. J. Dobbsa.
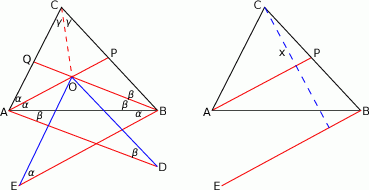
Dorysujmy odcinki  ,
, 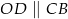 ,
, 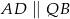 i
i 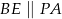 . W trapezie
. W trapezie 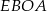 przekątne są nachylone pod tym samym kątem do podstawy, więc jest on równoramienny, czyli
przekątne są nachylone pod tym samym kątem do podstawy, więc jest on równoramienny, czyli 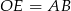 . Podobnie
. Podobnie 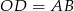 . Zatem punkty
. Zatem punkty 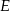 i
i 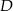 są położone symetrycznie względem dwusiecznej
są położone symetrycznie względem dwusiecznej 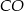 kąta
kąta 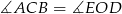 .
.
Jeżeli teraz oznaczymy przez  i
i 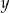 odległości punktu
odległości punktu 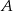 od prostych
od prostych 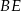 i
i 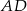 odpowiednio, to
odpowiednio, to
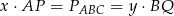
(pierwsza równość jest wyjaśniona na drugim rysunku – należy myśleć o sumie pól trójkątów 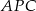 i
i 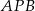 , z drugą jest podobnie). Jeżeli zatem założymy, że
, z drugą jest podobnie). Jeżeli zatem założymy, że 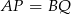 to mamy
to mamy 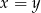 .
.
To oznacza, że 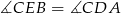 (bo
(bo 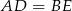 ). Ponieważ punkty
). Ponieważ punkty 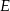 i
i 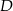 leżą symetrycznie względem dwusiecznej
leżą symetrycznie względem dwusiecznej 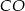 , daje to
, daje to 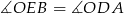 , czyli
, czyli 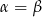 .
.
Udowodniony fakt nosi nazwę twierdzenia Steinera-Lehmusa i ma niezwykle barwną historię. Znanych jest kilkadziesiąt różnych dowodów tego twierdzenia, i praktycznie wszystkie są w pewnym stopniu dowodami nie wprost, tzn. używają nierówności między bokami trójkąta (w I z naszych dowód rozumowanie nie wprost jest na samym końcu przy opuszczaniu drugiego nawiasu, w III z dowodów, korzystamy z własności czworokątów wpisanych w okrąg, które też dowodzi się nie wprost; podobnie jest z czwartym dowodem). Według wybitnego geometry Johna Conwaya są przesłanki, że dowód wprost może nie istnieć. Argument Conwaya jest następujący: gdyby taki dowód był, to z ciągłości powinien zachować się gdy punkty 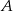 i
i 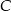 zbliżają się do siebie i dalej, mijają się. Algebraicznie oznacza to, że odcinek
zbliżają się do siebie i dalej, mijają się. Algebraicznie oznacza to, że odcinek 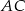 zaczyna mieć ujemną długość. Wtedy jednak łatwo jest podać kontrprzykład: można tak dobrać dane, żeby drugi z nawiasów w I sposobie się zerował.
zaczyna mieć ujemną długość. Wtedy jednak łatwo jest podać kontrprzykład: można tak dobrać dane, żeby drugi z nawiasów w I sposobie się zerował.

