/Konkursy/Zadania/Geometria/Planimetria/Trójkąt

Zadanie nr 3213679

Dodaj do ulubionych
Dodaj do rozwiązanych

Obwód trójkąta 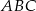ABC jest równy 8. Oblicz obwód trójkąta 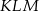KLM o wierzchołkach będących środkami środkowych trójkąta ABC .

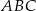Rozwiązanie

Rozpoczynamy od rysunku.

PIC

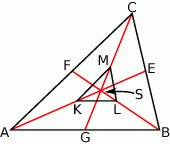
Wiemy, że punkt przecięcia środkowych dzieli je w stosunku 2:1 licząc od wierzchołka. Zatem

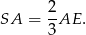
SA = 2AE . 3

Wiemy też, że 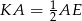KA = 12 AE . Stąd

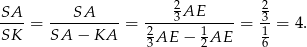
2 2 SA-- ---SA----- ----3AE------ 3- SK = SA − KA = 2AE − 1AE = 1 = 4. 3 2 6

Analogicznie uzasadniamy, że

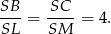
SB SC -SL = SM--= 4.

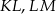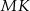To oznacza, że odcinki KL ,LM i MK są równoległe do odpowiednich boków trójkąta 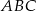ABC oraz

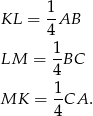
1 KL = -AB 4 LM = 1BC 4 1- MK = 4CA .

Zatem obwód trójkąta 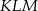KLM jest 4 razy mniejszy od obwodu trójkąta ABC .  
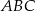Odpowiedź: 2

Wersja PDF