Zadanie nr 6829877
Funkcja 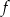 jest funkcją okresową o okresie zasadniczym
jest funkcją okresową o okresie zasadniczym 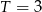 i w przedziale
i w przedziale 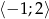 określona jest wzorem
określona jest wzorem 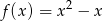 .
.
- Naszkicuj wykres funkcji dla
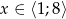 .
. - Oblicz sumę wszystkich dodatnich miejsc zerowych funkcji
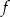 mniejszych od 200.
mniejszych od 200.
Rozwiązanie
- Z rysowaniem wykresu nie powinno być problemu – rysujemy funkcję
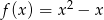 na przedziale
na przedziale 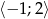 i narysowany wykres przesuwamy dwa razy w prawo. Na koniec zostawiamy tylko kawałek nad przedziałem
i narysowany wykres przesuwamy dwa razy w prawo. Na koniec zostawiamy tylko kawałek nad przedziałem 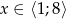
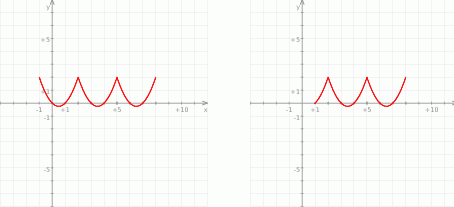
- Z rysowanego wykresu, lub ze wzoru funkcji widać, że dodatnie miejsca zerowe funkcji to
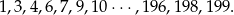
Mamy tu dwa ciągi arytmetyczne
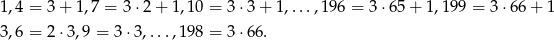
Ich sumy wynoszą odpowiednio
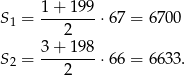
Łącznie mamy więc
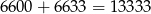 .
.
Odpowiedź: 13333

