Zadanie nr 8405309
Funkcja 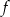 przyporządkowuje każdej liczbie naturalnej dodatniej liczbę jej dzielników będących liczbami pierwszymi. Np.
przyporządkowuje każdej liczbie naturalnej dodatniej liczbę jej dzielników będących liczbami pierwszymi. Np. 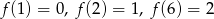 .
.
- Naszkicuj wykres funkcji
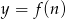 dla
dla 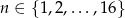 .
. - Podaj przykład liczby
 , dla której
, dla której 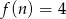 .
. - Uzasadnij, że równanie
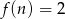 ma nieskończenie wiele rozwiązań.
ma nieskończenie wiele rozwiązań.
Rozwiązanie
- Rysujemy (dla każdej liczby
 z podanego zbioru liczymy ile ma ona dzielników pierwszych).
z podanego zbioru liczymy ile ma ona dzielników pierwszych). 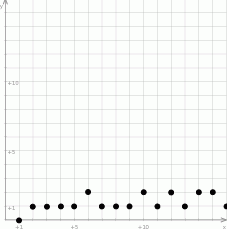
- Np.
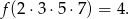
Odpowiedź: Np.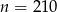
- Wiadomo, że jest nieskończenie wiele liczb pierwszych. Jeżeli
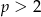 jest dowolną liczbą pierwszą to liczba
jest dowolną liczbą pierwszą to liczba 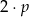 ma tylko dwa dzielniki pierwsze: 2 i
ma tylko dwa dzielniki pierwsze: 2 i 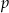 . Zatem
. Zatem