Dany jest ciąg arytmetyczny 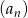 dla
dla 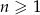 , w którym
, w którym 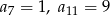 .
.
- Oblicz pierwszy wyraz
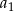 i różnicę
i różnicę  ciągu
ciągu 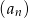 .
. - Sprawdź, czy ciąg
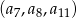 jest geometryczny.
jest geometryczny. - Wyznacz takie
 , aby suma
, aby suma  początkowych wyrazów ciągu
początkowych wyrazów ciągu 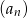 miała wartość najmniejszą.
miała wartość najmniejszą.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dany jest ciąg arytmetyczny 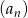 dla
dla 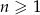 , w którym
, w którym 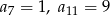 .
.
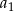 i różnicę
i różnicę  ciągu
ciągu 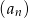 .
. 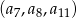 jest geometryczny.
jest geometryczny.  , aby suma
, aby suma  początkowych wyrazów ciągu
początkowych wyrazów ciągu 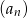 miała wartość najmniejszą.
miała wartość najmniejszą.Dany jest ciąg arytmetyczny 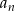 w którym
w którym 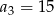 oraz
oraz 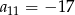 .
.
 zachodzi równość
zachodzi równość 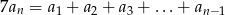 ?
? 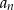 , które są podzielne przez 3.
, które są podzielne przez 3.Iloczyn pierwszego i szóstego wyrazu malejącego ciągu arytmetycznego o wyrazach całkowitych jest równy 100. Przy dzieleniu wyrazu drugiego przez wyraz szósty otrzymujemy 3 i resztę 2. Oblicz, o ile jest mniejsza suma dwustu początkowych wyrazów o numerach parzystych od sumy dwustu początkowych wyrazów tego ciągu o numerach nieparzystych.
W ciągu arytmetycznym 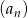 o różnicy
o różnicy 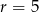 dane są:
dane są: 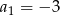 i
i 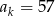 . Wyznacz liczbę
. Wyznacz liczbę 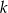 oraz oblicz sumę
oraz oblicz sumę 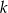 początkowych wyrazów ciągu
początkowych wyrazów ciągu 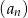
Czwarty wyraz ciągu arytmetycznego jest równy 6. Oblicz sumę siedmiu początkowych wyrazów tego ciągu.
W malejącym ciągu arytmetycznym 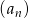 spełnione są warunki
spełnione są warunki 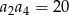 oraz
oraz 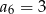 . Wyznacz sumę 10 początkowych wyrazów tego ciągu.
. Wyznacz sumę 10 początkowych wyrazów tego ciągu.
