Cena biletu na mecz piłki nożnej wynosiła 150 zł. Gdy cenę obniżono okazało się, że na mecz przychodziło 50% więcej kibiców, a dochód uzyskany ze sprzedaży wzrósł o 25%. O ile złotych obniżono cenę biletu?
/Szkoła podstawowa
Cena biletu na mecz piłki nożnej wynosiła 60zł. Gdy cenę obniżono okazało się, że na mecz przychodziło 20% więcej kibiców, a dochód uzyskany ze sprzedaży wzrósł o 10%. O ile złotych obniżono cenę biletu?
Wartość wyrażenia 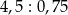 jest równa wartości wyrażenia A/B.
jest równa wartości wyrażenia A/B.
A) 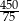 B)
B) 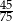
Wartość wyrażenia 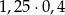 jest równa wartości wyrażenia C/D.
jest równa wartości wyrażenia C/D.
C) 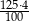 D)
D) 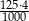
Ile jest wszystkich czterocyfrowych liczb naturalnych mniejszych niż 2017?
A) 2016 B) 2017 C) 1016 D) 1017
Ile jest wszystkich czterocyfrowych liczb naturalnych większych niż 2018?
A) 7979 B) 7980 C) 7981 D) 7982
Zaczynając od punktu 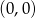 budujemy łamaną, której część składającą się z 6 odcinków przedstawiono na rysunku. Kolejne odcinki łamanej numerujemy kolejnymi liczbami naturalnymi. Drugi odcinek łamanej ma długość 2.
budujemy łamaną, której część składającą się z 6 odcinków przedstawiono na rysunku. Kolejne odcinki łamanej numerujemy kolejnymi liczbami naturalnymi. Drugi odcinek łamanej ma długość 2.
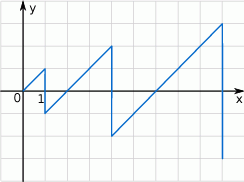
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Jeżeli  jest liczbą nieparzystą, to odcinek o numerze jest liczbą nieparzystą, to odcinek o numerze  jest równoległy doodcinka o numerze 1. jest równoległy doodcinka o numerze 1. | P | F |
Jeżeli  jest liczbą parzystą, to długość odcinka o numerze jest liczbą parzystą, to długość odcinka o numerze  jest równa jest równa 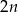 . . | P | F |
Zaczynając od punktu 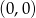 budujemy łamaną, której część składającą się z 6 odcinków przedstawiono na rysunku. Kolejne odcinki łamanej numerujemy kolejnymi liczbami naturalnymi. Drugi odcinek łamanej ma długość 2.
budujemy łamaną, której część składającą się z 6 odcinków przedstawiono na rysunku. Kolejne odcinki łamanej numerujemy kolejnymi liczbami naturalnymi. Drugi odcinek łamanej ma długość 2.
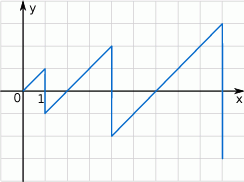
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Długość odcinka o numerze 5 jest równa 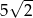 . . | P | F |
Jeżeli  jest liczbą parzystą, to długość odcinka o numerze jest liczbą parzystą, to długość odcinka o numerze 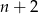 jest o 2 większa od długości odcinka o numerze jest o 2 większa od długości odcinka o numerze  . . | P | F |
Zaczynając od punktu 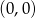 budujemy łamaną, której część składającą się z 6 odcinków przedstawiono na rysunku. Kolejne odcinki łamanej numerujemy kolejnymi liczbami naturalnymi. Drugi odcinek łamanej ma długość 2.
budujemy łamaną, której część składającą się z 6 odcinków przedstawiono na rysunku. Kolejne odcinki łamanej numerujemy kolejnymi liczbami naturalnymi. Drugi odcinek łamanej ma długość 2.
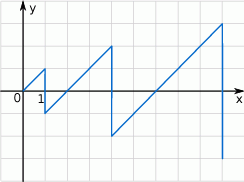
Wierzchołek łamanej, którego druga współrzędna jest równa 2013 jest punktem wspólnym odcinków łamanej o numerach
A) 2012 i 2013 B) 2013 i 2014 C) 4025 i 4026 D) 4026 i 4027
Zapisano sumę szesnastu jednakowych składników:
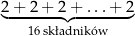
Wartość tej sumy jest równa
A) 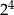 B)
B) 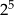 C)
C) 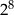 D)
D) 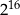
Paweł i Michał zostali wynajęci do namalowania białych linii po obu stronach ulicy Akacjowej. Paweł przyszedł pierwszy i zdążył namalować trzy metry linii po prawej stronie, zanim nadszedł Michał i zasugerował, żeby Paweł zajął się lewą stroną. Paweł zaczął więc od początku, po lewej stronie, a Michał kontynuował po prawej. Kiedy Michał skończył swoją stronę, przeszedł przez jezdnię i domalował brakujące sześć metrów Pawła. Długość obu stron ulicy była taka sama. Kto namalował dłuższą linie i o ile?
Cegielnia sprzedaje cegły pakowane w paletach po 330 sztuk. Gdyby ułożyć wszystkie cegły z jednej palety jedna za drugą, to łączna ich długość wyniosłaby 82,5 m. Ile cegieł należałoby ułożyć jedna za drugą, aby ich łączna długość wynosiła 1,5 km? Ile palet należałoby zamówić, aby kupić taką liczbę cegieł?
Z drewnianych listewek, które mają kształt prostopadłościanu o podstawie 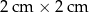 zbudowany drewniany szkielet przedstawiony na rysunku.
zbudowany drewniany szkielet przedstawiony na rysunku.
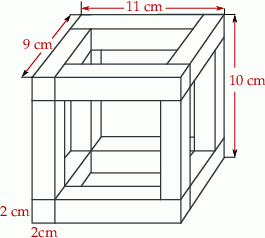
Suma długości listewek, z których zbudowano szkielet jest równa A/B.
A) 120 cm B) 88 cm
Objętość drewna użytego do budowy szkieletu jest równa C/D.
C) 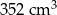 D)
D) 
W szufladzie jest 7 par skarpetek białych i 3 pary skarpetek czarnych. Tomek losuje z szuflady po jednej skarpetce i kładzie ją na stół.
Zaznacz P, jeśli zdanie jest prawdziwe, lub zaznacz F – jeśli jest fałszywe.
| Prawdopodobieństwo wylosowania czarnej skarpetki jest równe 0,3. | P | F |
| Tomek za pierwszym razem nie wylosował czarnej skarpetki. Prawdopodobieństwo, że za drugim razem wylosuje czarną skarpetkę jest większe. | P | F |
W pudełku znajduje się 18 losów, wśród których są 2 losy wygrywające.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Prawdopodobieństwo wyciągnięcia losu przegrywającego jest dziewięciokrotnie większe, niż wyciągnięcia losu wygrywającego. | P | F |
| Jeżeli do pudełka włożymy dwa losy wygrywające to prawdopodobieństwo wygranej wzrośnie o 100%. | P | F |
W pudełku jest 30 kul białych i 20 czarnych. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Jeżeli 10 kul białych zostanie zastąpionych kulami czarnymi, to prawdopodobieństwa wylosowania kuli czarnej i białej będą równe. | P | F |
| Jeżeli podwoimy liczbę kul czarnych w pudełku, to prawdopodobieństwo wylosowania kuli czarnej wzrośnie dwukrotnie. | P | F |
W pudełku było 15 kul białych i 5 czarnych. Dołożono jeszcze 10 kul białych i 20 czarnych. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Przed dołożeniem kul prawdopodobieństwo wylosowania kuli białej było trzy razy większe niż prawdopodobieństwo wylosowania kuli czarnej. | P | F |
| Po dołożeniu kul prawdopodobieństwo wylosowania kuli czarnej jest większe niż prawdopodobieństwo wylosowania kuli białej. | P | F |
W pudełku znajduje się 6 losów, wśród których są 2 losy wygrywające.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Prawdopodobieństwo wyciągnięcia losu wygrywającego jest dwukrotnie mniejsze, niż wyciągnięcia losu przegrywającego. | P | F |
| Jeśli do pudełka włożymy dodatkowy los wygrywający, to prawdopodobieństwo wygranej wzrośnie. | P | F |
W pudełku było 20 kul białych i 10 czarnych. Dołożono jeszcze 10 kul białych i 15 czarnych. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Przed dołożeniem kul prawdopodobieństwo wylosowania kuli białej było trzy razy większe niż prawdopodobieństwo wylosowania kuli czarnej. | P | F |
| Po dołożeniu kul prawdopodobieństwo wylosowania kuli czarnej jest większe niż prawdopodobieństwo wylosowania kuli białej. | P | F |
W szufladzie znajduje się 10 par skarpetek, w tym 3 pary skarpetek czarnych. Tomek losowo wyjmuje po jednej skarpetce z szuflady.
Wybierz P, jeśli zdanie jest prawdziwe, lub F jeśli jest fałszywe.
| Tomek, aby mieć pewność, że przynajmniej dwie wyjęte skarpetki będą czarne, musi wyjąć co najmniej 16 skarpetek. | P | F |
| Tomek za pierwszym razem nie wyjął czarnej skarpetki. Prawdopodobieństwo, że za drugim razem wyjmie czarną skarpetkę, wzrosło. | P | F |
Do pudełka włożono piłki zielone i czerwone. Wszystkich piłek jest 8, a piłek czerwonych jest 6.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Prawdopodobieństwo wyciągnięcia czerwonej piłki jest trzy razy większe, niż prawdopodobieństwo wyciągnięcia piłki zielonej. | P | F |
| Jeśli z pudełka zabierzemy 2 czerwone piłki, to prawdopodobieństwa wyciągnięcia piłki czerwonej i zielonej będą równe. | P | F |
Siatka ostrosłupa składa się z kwadratu i trójkątów równobocznych zbudowanych na bokach tego kwadratu.
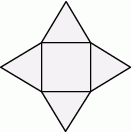
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Wszystkie krawędzie tego ostrosłupa mają taką samą długość. | P | F |
| Wysokość tego ostrosłupa jest mniejsza niż wysokość jego ściany bocznej. | P | F |
Siatka ostrosłupa składa się z czterech trójkątów równobocznych.
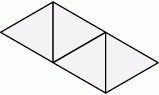
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Ostrosłup ten ma 6 krawędzi. | P | F |
| Wysokość tego ostrosłupa jest równa długości jego krawędzi. | P | F |
Czy z odcinków o długościach: 4 cm, 4 cm, 9 cm można zbudować trójkąt?
Czy z odcinków o długościach: 4 cm, 4 cm, 2 cm można zbudować trójkąt?
Czy z odcinków o długościach: 3 cm, 7 cm, 4 cm można zbudować trójkąt?
Czy z odcinków o długościach: 11 cm, 8 cm, 17 cm można zbudować trójkąt?
Czy z odcinków o długościach: 8 cm, 13 cm, 20 cm można zbudować trójkąt?
Czy z odcinków o długościach: 13 cm, 8 cm, 5 cm można zbudować trójkąt?
Czy z odcinków o długościach: 3 cm, 3 cm, 3 cm można zbudować trójkąt?
Z kwadratowego kartonika odcięto naroża, tak jak pokazano na rysunku i otrzymano ośmiokąt foremny o bokach długości 4.
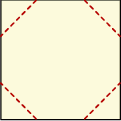
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Kartonik był kwadratem o boku 12. | P | F |
| Suma pól odciętych naroży jest równa 16. | P | F |
Z kwadratowego kartonika o boku długości 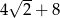 odcięto naroża, tak jak pokazano na rysunku i otrzymano ośmiokąt foremny.
odcięto naroża, tak jak pokazano na rysunku i otrzymano ośmiokąt foremny.
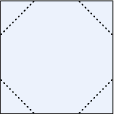
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Bok ośmiokąta ma długość 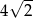 . . | P | F |
| Suma pól odciętych naroży jest równa 24. | P | F |
Z kwadratowego kartonika odcięto naroża, tak jak pokazano na rysunku i otrzymano ośmiokąt foremny o bokach długości 2.
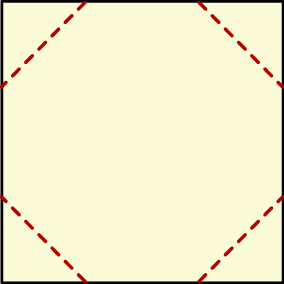
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Kartonik był kwadratem o polu 36. | P | F |
| Suma pól odciętych naroży jest równa 8. | P | F |
W trójkącie prostokątnym jedna z przyprostokątnych ma długość 15 cm, a przeciwprostokątna jest o 9 cm dłuższa od drugiej przyprostokątnej. Oblicz pole tego trójkąta oraz długość wysokości poprowadzonej z wierzchołka kąta prostego.
W trójkącie prostokątnym jedna z przyprostokątnych ma długość 10 cm, a przeciwprostokątna jest o 2 cm dłuższa od drugiej przyprostokątnej. Oblicz pole tego trójkąta oraz długość wysokości poprowadzonej z wierzchołka kąta prostego.
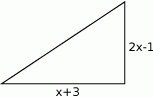
Pole trójkąta przedstawionego na rysunku jest równe 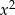 . Oblicz
. Oblicz  .
.
Liczby 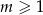 i
i 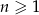 spełniają warunek
spełniają warunek 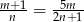 . Wtedy liczba
. Wtedy liczba  jest równa
jest równa
A) 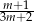 B)
B) 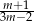 C)
C) 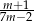 D)
D) 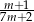
Wiadomo, że liczba 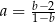 dla
dla 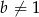 . Zatem
. Zatem
A) 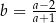 B)
B) 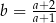 C)
C) 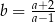 D)
D) 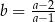
Wiadomo, że liczba 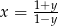 dla
dla 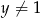 . Zatem
. Zatem
A) 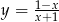 B)
B) 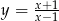 C)
C) 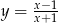 D)
D) 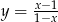
Adam i Wojtek mają razem 82 cukierki. Jeżeli każdy z chłopców zje 29 cukierków, to Adam będzie miał trzy razy mniej cukierków niż Wojtek.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Jeżeli Wojtek odda Adamowi 6 cukierków, to chłopcy będą mieli taką samą liczbę cukierków. | P | F |
| Jeżeli każdy z chłopców zje 23 cukierki, to Wojtek będzie miał dwa razy więcej cukierków niż Adam. | P | F |
Pociąg o długości 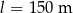 przejechał przez tunel o długości
przejechał przez tunel o długości 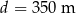 ze stałą prędkością
ze stałą prędkością 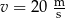 .
.
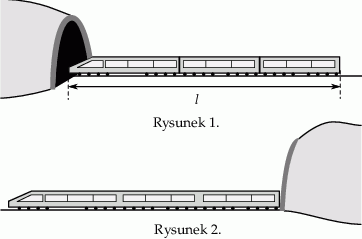
Ile czasu upłynęło od momentu wjazdu czoła pociągu do tunelu (rysunek 1.) do momentu wyjazdu z tunelu końca ostatniego wagonu (rysunek 2.)?
A) 7,5 s B) 17,5 s C) 25 s D) 36 s
Pociąg o długości 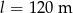 przejechał przez most o długości
przejechał przez most o długości 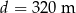 ze stałą prędkością
ze stałą prędkością 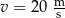 .
.
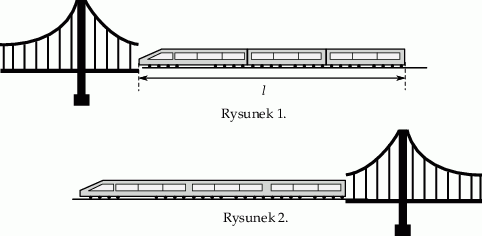
Ile czasu upłynęło od momentu wjazdu czoła pociągu na most (rysunek 1.) do momentu zjazdu z mostu końca ostatniego wagonu (rysunek 2.)?
A) 6 s B) 16 s C) 25 s D) 22 s
Na rysunkach I–IV przedstawiono cztery pary trójkątów.
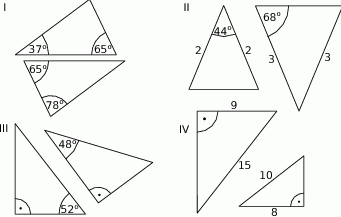
Na którym rysunku trójkąty nie są podobne?
A) I B) II C) III D) IV
Zaznacz zdanie fałszywe.
A) Liczba krawędzi każdego ostrosłupa jest liczbą parzystą.
B) Liczba krawędzi każdego graniastosłupa dzieli się przez 3.
C) Liczba krawędzi każdego ostrosłupa dzieli się przez 3.
D) Liczba wierzchołków każdego graniastosłupa jest liczbą parzystą.
Ostrosłup i graniastosłup mają takie same podstawy. Obie bryły mają łącznie 25 wierzchołków. Ile wierzchołków ma ostrosłup?
A) 6 B) 8 C) 9 D) 10
W kapeluszu znajdują się króliki białe i szare. Królików szarych jest trzy razy więcej niż białych. Prawdopodobieństwo wyciągnięcia z kapelusza królika białego jest równe  . Zatem prawdopodobieństwo wyciągnięcia z kapelusza królika szarego jest równe
. Zatem prawdopodobieństwo wyciągnięcia z kapelusza królika szarego jest równe
A) 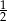 B)
B) 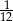 C)
C) 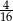 D)
D) 
W woreczku znajdują się piłki białe i szare. Piłek szarych jest trzy razy więcej niż białych. Prawdopodobieństwo wyciągnięcia z woreczka piłki białej jest równe 0,25. Zatem prawdopodobieństwo wyciągnięcia z woreczka piłki szarej jest równe
A) 0,75 B) 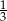 C) 0,25 D) 0,8
C) 0,25 D) 0,8
W kapeluszu znajdują się króliki białe i szare. Prawdopodobieństwo wyciągnięcia z kapelusza królika szarego jest równe 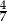 . Zatem prawdopodobieństwo wyciągnięcia z kapelusza królika białego jest równe
. Zatem prawdopodobieństwo wyciągnięcia z kapelusza królika białego jest równe
A)  B) 0,75 C)
B) 0,75 C)  D)
D)