Z takiego samego rodzaju stearyny wykonano dwie świece: pierwszą w kształcie graniastosłupa prostego o podstawie kwadratu i drugą w kształcie graniastosłupa prostego o podstawie trójkąta równobocznego. Pole podstawy pierwszej świecy jest o 25% większe niż pole podstawy drugiej świecy, a wysokość drugiej świecy jest o 30% większa niż wysokość pierwszej świecy. Łączna waga obu świec to 0,51 kg. Oblicz jaka jest waga każdej ze świec.
/Szkoła podstawowa
W tabeli poniżej przedstawione są wyniki pracy klasowej w dwóch klasach pierwszych.
| Ocena | 3,25 | 2,75 | 4,25 | 4 | 2 | 5,25 | 3,75 | 4,75 | 1 | 3 | 5 | 2,25 | 6 | 5,75 |
| Liczba ocen | 2 | 5 | 2 | 1 | 5 | 1 | 3 | 2 | 1 | 4 | 3 | 1 | 2 | 3 |
Mediana ocen w tych dwóch klasach jest równa
A) 4 B) 3 C) 3,25 D) 3,75
Drewniany stożek przecięto na dwie części płaszczyzną równoległą do podstawy i przechodzącą przez środek wysokości stożka.
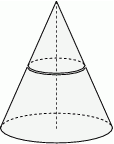
Stosunek masy dolnej części do masy górnej części jest równy
A) 7 B) 8 C) 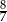 D) 3
D) 3
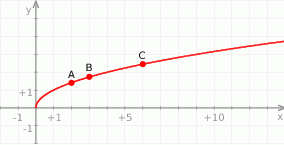
Na rysunku przedstawiono wykres funkcji 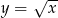 oraz zaznaczono trzy punkty tego wykresu:
oraz zaznaczono trzy punkty tego wykresu: 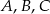 . Wyznacz współrzędne tych punktów.
. Wyznacz współrzędne tych punktów.
Paweł zamówił szybę w kształcie rombu o przekątnych 40 cm i 30 cm. Zaproponował szklarzowi, by wyciął romb z prostokątnego kawałka szyby, tak jak na rysunku. Jakie wymiary ma ten prostokątny kawałek szyby?
Figurami podobnymi są figury
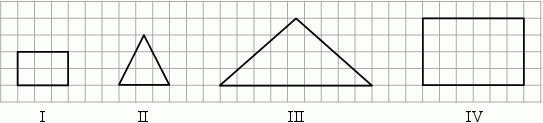
A) I i II B) II i III C) III i IV D) I i IV
Figurami podobnymi są figury
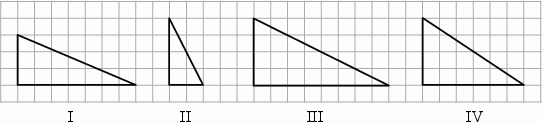
A) I i II B) II i III C) III i IV D) I i IV
Wymień ujemne liczby wymierne większe od 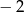 , które można przedstawić w postaci ułamka o całkowitym liczniku i mianowniku równym 3.
, które można przedstawić w postaci ułamka o całkowitym liczniku i mianowniku równym 3.
Wymień dodatnie liczby wymierne mniejsze od 4, które można przedstawić w postaci pierwiastka kwadratowego z liczby naturalnej.
Obwód podstawy ostrosłupa prawidłowego siedmiokątnego jest równy 33,6 cm, a długość jego krawędzi bocznej jest równa 2,5 cm. Pole powierzchni bocznej tego ostrosłupa jest równe
A) 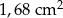 B)
B) 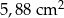 C)
C) 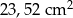 D)
D) 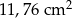
Puszki z przecierem pomidorowym mają kształt walca o średnicy podstawy 4 cm oraz wysokości 3 cm. Puszki te mogą być na kilka sposobów zapakowane ciasno po 4 sztuki w prostopadłościenne tekturowe pudełka. Wybierz jeden z możliwych sposobów zapakowania puszek, zrób odręczny rysunek siatki odpowiedniego prostopadłościanu i podaj długości krawędzi tego prostopadłościanu.
Dwie proste równoległe 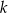 i
i 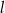 przecięto prostymi
przecięto prostymi 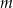 i
i  w sposób przedstawiony na rysunku.
w sposób przedstawiony na rysunku.
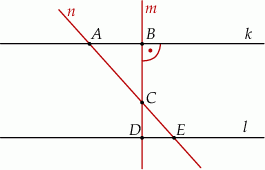
Czy trójkąty  i
i  są podobne? Wybierz odpowiedź T albo N oraz jej uzasadnienie spośród zdań oznaczonych literami A–C.
są podobne? Wybierz odpowiedź T albo N oraz jej uzasadnienie spośród zdań oznaczonych literami A–C.
| Tak | Nie |
| ponieważ | |
| A) | te trójkąty mają wspólny wierzchołek. |
| B) | te trójkąty mają boki różnej długości. |
| C) | te trójkąty mają odpowiednie kąty równej miary. |
Dwie proste równoległe  i
i 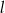 przecięto prostymi
przecięto prostymi 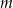 i
i  w sposób przedstawiony na rysunku.
w sposób przedstawiony na rysunku.
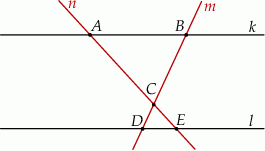
Czy trójkąty 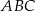 i
i 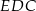 są przystające? Wybierz odpowiedź T albo N oraz jej uzasadnienie spośród zdań oznaczonych literami A–D.
są przystające? Wybierz odpowiedź T albo N oraz jej uzasadnienie spośród zdań oznaczonych literami A–D.
| Tak | Nie |
| ponieważ | |
| A) | te trójkąty mają wspólny wierzchołek. |
| B) | te trójkąty mają boki różnej długości. |
| C) | te trójkąty mają odpowiednie kąty równej miary. |
| D) | te trójkąty mają boki równoległe. |
Dwie proste równoległe 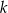 i
i 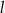 przecięto prostymi
przecięto prostymi 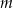 i
i  w sposób przedstawiony na rysunku.
w sposób przedstawiony na rysunku.
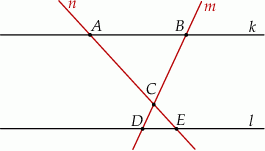
Czy trójkąty  i
i 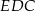 są podobne? Wybierz odpowiedź T albo N oraz jej uzasadnienie spośród zdań oznaczonych literami A–D.
są podobne? Wybierz odpowiedź T albo N oraz jej uzasadnienie spośród zdań oznaczonych literami A–D.
| Tak | Nie |
| ponieważ | |
| A) | te trójkąty mają wspólny wierzchołek. |
| B) | te trójkąty mają boki różnej długości. |
| C) | te trójkąty mają odpowiednie kąty równej miary. |
| D) | te trójkąty są przystające. |
Na którym rysunku narysowano średnicę okręgu?

Jedenaście piłeczek, ponumerowanych kolejnymi liczbami naturalnymi od 1 do 11, wrzucono do pudełka. Janek, nie patrząc na piłeczki, wyjmuje je z pudełka. Ile najmniej piłeczek musi wyjąć Janek, aby mieć pewność, że przynajmniej jedna wyjęta piłeczka jest oznaczona liczbą parzystą? Odpowiedź uzasadnij.
Trzydzieści piłeczek, ponumerowanych kolejnymi liczbami naturalnymi od 1 do 30, wrzucono do pudełka. Kacper, nie patrząc na piłeczki, wyjmuje je z pudełka. Ile najmniej piłeczek musi wyjąć Kacper, aby mieć pewność, że przynajmniej jedna wyjęta piłeczka jest oznaczona liczbą podzielną przez 4? Odpowiedź uzasadnij.
W szufladzie znajduje się 26 różnych par skarpet. Zosia nie zaglądając do szuflady wyjmuje z niej po jednej skarpetce. Ile co najmniej skarpet musi wyjąć Zosia, aby mieć pewność, że wśród wyjętych skarpet są przynajmniej dwie kompletne pary? Odpowiedź uzasadnij.
Z trzech jednakowych klocków w kształcie sześcianu i jednego klocka w kształcie ostrosłupa prawidłowego czworokątnego zbudowano dwie wieże (zobacz rysunek).
Krawędź sześcianu ma długość 10 cm. Krawędź podstawy ostrosłupa prawidłowego czworokątnego ma długość 9 cm, a jego objętość jest równa 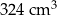 . Oblicz różnicę wysokości obu wież.
. Oblicz różnicę wysokości obu wież.
Obwód czworokąta wypukłego 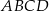 jest równy 50 cm. Obwód trójkąta
jest równy 50 cm. Obwód trójkąta 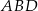 jest równy 46 cm, a obwód trójkąta
jest równy 46 cm, a obwód trójkąta 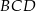 jest równy 36 cm. Oblicz długość przekątnej
jest równy 36 cm. Oblicz długość przekątnej 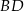 .
.
Dany jest trapez prostokątny 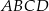 , w którym
, w którym 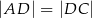 oraz
oraz 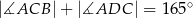 (zobacz rysunek).
(zobacz rysunek).
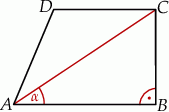
Stąd wynika, że
A) 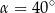 B)
B) 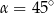 C)
C) 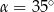 D)
D) 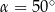
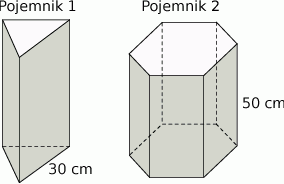
Dwa pojemniki mają kształt graniastosłupów prawidłowych, przy czym pierwszy ma kształt graniastosłupa trójkątnego o krawędzi podstawy długości 30 cm, a drugi sześciokątnego o wysokości 50 cm. Objętość pierwszego pojemnika stanowi 45% objętości drugiego pojemnika i jest mniejsza od tej objętości o 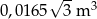 . Oblicz objętości obu pojemników.
. Oblicz objętości obu pojemników.
Napisz wzór funkcji liniowej o współczynniku kierunkowym 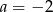 , której wykres przecina oś
, której wykres przecina oś 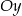 w punkcie
w punkcie 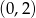 . Wyznacz miejsce zerowe tej funkcji.
. Wyznacz miejsce zerowe tej funkcji.
Napisz wzór funkcji liniowej o współczynniku kierunkowym 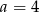 , której wykres przecina oś
, której wykres przecina oś 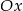 w punkcie
w punkcie 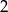 . Wyznacz punkt przecięcia wykresu z osią
. Wyznacz punkt przecięcia wykresu z osią 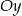 .
.
Napisz wzór funkcji liniowej, której wykres jest równoległy do wykresu funkcji 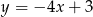 i przecina oś
i przecina oś 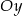 w punkcie
w punkcie 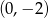 .
.
Długość modelu samolotu Albatros D.V wykonanego w skali 1:48 wynosi 153 mm. Długość samolotu Albatros D.V wynosi około
A) 7,34 m B) 74 m C) 0,74 m D) 7,4 m
Na planie miasta odległość w linii prostej od punktu oznaczającego przystanek autobusowy Uniwersytet do punktu oznaczającego przystanek autobusowy Muzeum jest równa 12 cm. Plan miasta został wykonany w skali 1 : 5 000.
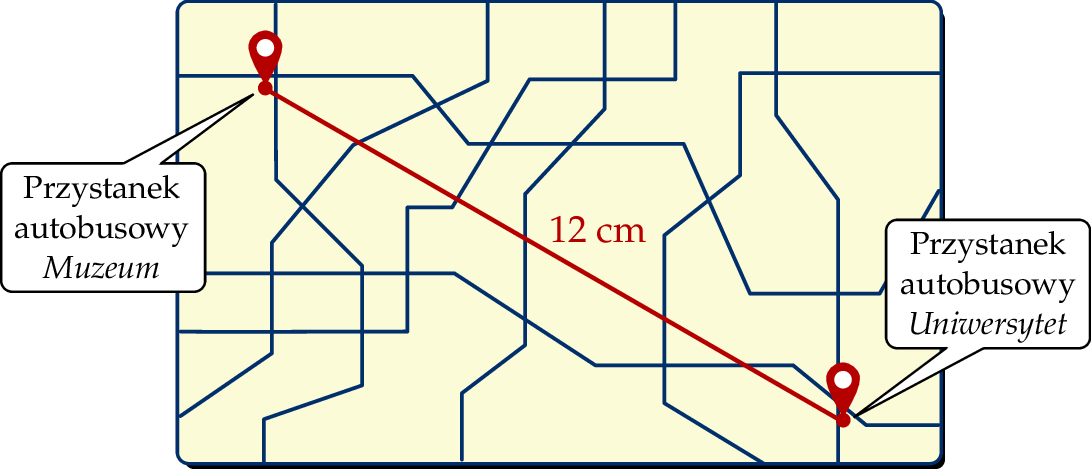
Odległość w linii prostej w terenie między tymi przystankami jest równa
A) 2 400 m B) 600 m C) 3 200 m D) 6 000m
Na planie miasta wykonanym w skali 1:5000 odległość w linii prostej między punktem oznaczającym wejście do papugarni a punktem oznaczającym wejście do muzeum zabawek jest równa 8,4 cm. W terenie odległość między wejściami do tych obiektów jest w linii prostej równa
A) 4,2 m B) 42 m C) 420 m D) 4200 m
Na planie miasta odległość w linii prostej od punktu oznaczającego przystanek autobusowy Dworzec do punktu oznaczającego przystanek autobusowy Galeria jest równa 8 cm. Plan miasta został wykonany w skali 1 : 4 000.
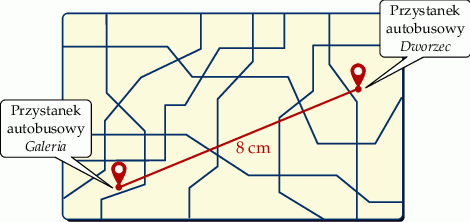
Odległość w linii prostej w terenie między tymi przystankami jest równa
A) 320 m B) 500 m C) 3 200 m D) 5 000m
Oblicz 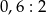 .
.
Oblicz 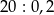 .
.
Oblicz 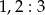 .
.
Oblicz 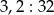 .
.
Oblicz 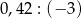 .
.
Oblicz 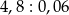 .
.
Oblicz 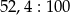 .
.
Wykres przedstawia zależność drogi przebytej przez samochód jadący z miasta 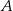 do miasta
do miasta 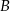 w zależności od czasu jazdy.
w zależności od czasu jazdy.
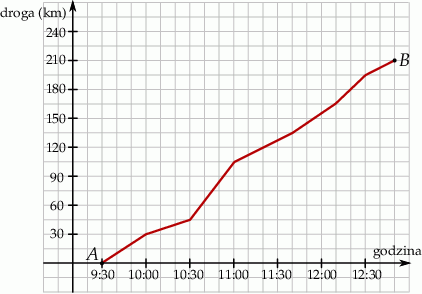
Zaznacz P, jeśli zdanie jest prawdziwe, lub zaznacz F – jeśli jest fałszywe.
| Samochód przejechał drugą połowę trasy szybciej niż pierwszą połowę. | P | F |
| Pół godziny przez zakończeniem podróży samochód miał jeszcze do przejechania 30 km. | P | F |
Wykres przedstawia zależność drogi przebytej przez samochód jadący z miasta  do miasta
do miasta  w zależności od czasu jazdy.
w zależności od czasu jazdy.
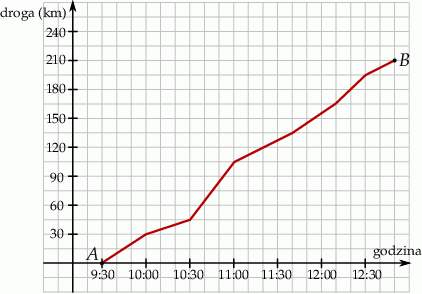
Z jaką największą prędkością poruszał się samochód?
A) 150 km/h B) 90 km/h C) 60 km/h D) 120 km/h

