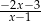Kąt ostry rombu ma miarę 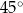 , a jego bok ma długość
, a jego bok ma długość  .
.
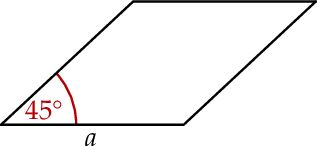
Pole tego rombu można wyrazić wzorem
A) 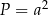 B)
B) 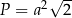 C)
C) 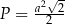 D)
D) 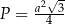
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Kąt ostry rombu ma miarę 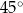 , a jego bok ma długość
, a jego bok ma długość  .
.

Pole tego rombu można wyrazić wzorem
A) 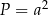 B)
B) 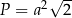 C)
C) 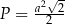 D)
D) 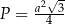
Wskaż liczbę, której 4% jest równe 8.
A) 3,2 B) 32 C) 100 D) 200
Wskaż liczbę, której 6% jest równe 6.
A) 0,36 B) 3,6 C) 10 D) 100
Jeżeli 8,5% liczby  jest równe 163,2, to liczba
jest równe 163,2, to liczba  jest równa
jest równa
A) 19200 B) 1920 C) 1387,2 D) 13872
4,5% liczby  jest równe 48,6. Liczba
jest równe 48,6. Liczba  jest równa
jest równa
A) 1080 B) 108 C) 48,6 D) 4,86
Wskaż liczbę, której 0,4% jest równe 12.
A) 0,048 B) 0,48 C) 30 D) 3000
Liczba 42 jest równa 0,6% liczby  . Wynika stąd, że
. Wynika stąd, że
A) 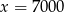 B)
B) 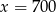 C)
C) 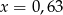 D)
D) 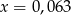
Jeżeli 35% pewnej liczby  jest równe 140 to
jest równe 140 to
A) 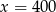 B)
B) 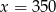 C)
C) 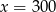 D)
D) 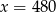
Liczba 78 stanowi 150% liczby  . Wtedy liczba
. Wtedy liczba  jest równa
jest równa
A) 60 B) 52 C) 48 D) 39
Liczba 609 stanowi 140% liczby  . Wtedy liczba
. Wtedy liczba  jest równa
jest równa
A) 420 B) 435 C) 468 D) 406
Dany jest prostokąt 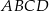 o wymiarach 12 cm i 16 cm. Odcinek
o wymiarach 12 cm i 16 cm. Odcinek 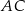 jest przekątną tego prostokąta. Odcinek
jest przekątną tego prostokąta. Odcinek 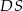 jest wysokością trójkąta
jest wysokością trójkąta 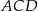 (patrz rysunek).
(patrz rysunek).
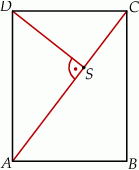
Oblicz długość odcinka 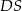 .
.
Dany jest prostokąt 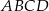 o wymiarach 10 cm i 24 cm. Odcinek
o wymiarach 10 cm i 24 cm. Odcinek 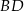 jest przekątną tego prostokąta. Odcinek
jest przekątną tego prostokąta. Odcinek 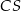 jest wysokością trójkąta
jest wysokością trójkąta 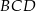 (patrz rysunek).
(patrz rysunek).
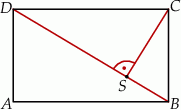
Oblicz długość odcinka 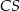 .
.
Oblicz pole i obwód trapezu prostokątnego przedstawionego na rysunku.
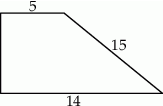
Oblicz pole i obwód trapezu prostokątnego przedstawionego na rysunku.
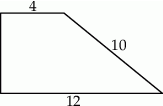
Kąty wewnętrzne przy wierzchołkach 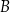 i
i 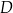 trapezu
trapezu 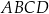 są równe odpowiednio
są równe odpowiednio 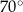 i
i 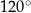 . Wówczas przedłużenia ramion
. Wówczas przedłużenia ramion 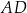 i
i 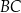 przecinają się pod kątem
przecinają się pod kątem
A) 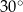 B)
B) 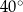 C)
C) 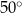 D)
D) 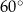
Kąty wewnętrzne przy wierzchołkach 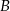 i
i 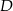 trapezu
trapezu 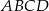 są równe odpowiednio
są równe odpowiednio 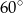 i
i 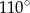 . Wówczas przedłużenia ramion
. Wówczas przedłużenia ramion 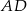 i
i 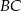 przecinają się pod kątem
przecinają się pod kątem
A) 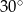 B)
B) 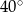 C)
C) 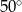 D)
D) 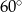
Długość przekątnej prostokąta przedstawionego na rysunku jest równa
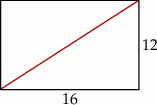
A) 12 B) 16 C) 18 D) 20
Średnia arytmetyczna ocen Jacka jest równa 3,75, a średnia ocen Karola (liczona z dokładnie tej samej liczby ocen) jest równa 4,25. Średnia ocen obu chłopców jest równa
A) 3,95 B) 4,5 C) 4,0 D) 4,15
Średnia arytmetyczna ocen Zosi jest równa 2,8, a średnia ocen Basi (liczona z dokładnie tej samej liczby ocen) jest równa 4,4. Średnia ocen obu dziewcząt jest równa
A) 3,6 B) 4,0 C) 3,8 D) 4,15
Na rysunku przedstawiono liczbę i rodzaj kul umieszczonych w każdym z czterech pudełek. Z każdego pudełka losujemy jedną kulę.
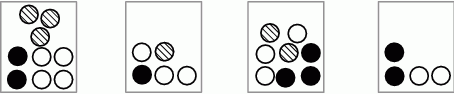
Prawdopodobieństwo wylosowania białej kuli jest największe, gdy kulę losujemy z pudełka
A) 1 B) 2 C) 3 D) 4
W tabeli przedstawiono liczbę i rodzaj kul umieszczonych w czterech pudełkach. Z każdego pudełka losujemy jedną kulę.
| Liczba kul zielonych | Liczba kul niebieskich | Liczba kul czerwonych | |
| Pudełko nr 1 | 4 | 8 | 5 |
| Pudełko nr 2 | 7 | 16 | 9 |
| Pudełko nr 3 | 2 | 7 | 3 |
| Pudełko nr 4 | 7 | 12 | 5 |
Prawdopodobieństwo wylosowania niebieskiej kuli jest największe, gdy kulę losujemy z pudełka nr
A) 1 B) 2 C) 3 D) 4
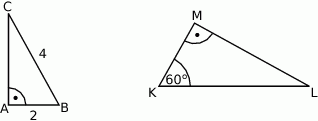
Uzasadnij, że trójkąty prostokątne 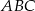 i
i 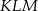 przedstawione na rysunku są podobne.
przedstawione na rysunku są podobne.
Zaokrąglij podaną liczbę do dziesiątek: 1 872,49.
Zaokrąglij podaną liczbę do dziesiątek: 432 755,2.
Zaokrąglij podaną liczbę do dziesiątek: 4 097,92.
Zaokrąglij podaną liczbę do dziesiątek: 6 396,2.
Zaokrąglij podaną liczbę do dziesiątek: 193,762.
Na seans filmowy sprzedano 280 biletów, w tym 126 ulgowych. Jaki procent sprzedanych biletów stanowiły bilety ulgowe?
A) 22% B) 33% C) 45% D) 63%
Na seans filmowy sprzedano 420 biletów, w tym 189 ulgowych. Jaki procent sprzedanych biletów stanowiły bilety ulgowe?
A) 63% B) 45% C) 33% D) 22%
Na seans filmowy sprzedano 280 biletów, w tym 84 ulgowych. Jaki procent sprzedanych biletów stanowiły bilety ulgowe?
A) 14% B) 22% C) 30% D) 42%
Na koncert sprzedano 680 biletów, w tym 306 na miejsca siedzące. Jaki procent sprzedanych biletów stanowiły bilety na miejsca siedzące?
A) 63% B) 45% C) 33% D) 22%
Ze zbiornika I, w którym znajdowało się 100 litrów wody, przelewano wodę do zbiornika II. Na wykresie przedstawiono, jak zmieniała się objętość wody w zbiorniku II od chwili, w której rozpoczęto przelewanie ze zbiornika I.
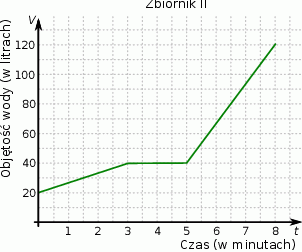
Ze zbiornika I, w którym znajdowało się 100 litrów wody, przelewano wodę do zbiornika II. Na wykresie przedstawiono, jak zmieniała się objętość wody w zbiorniku II od chwili, w której rozpoczęto przelewanie ze zbiornika I.
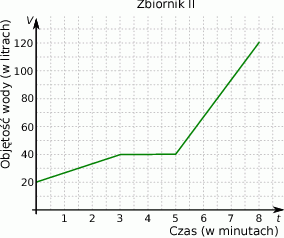
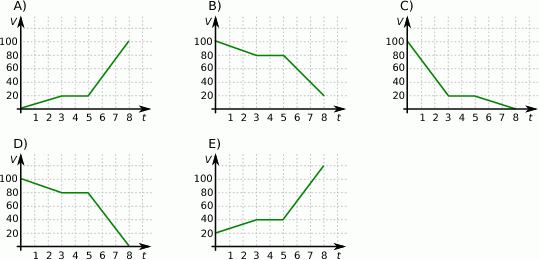
Na rysunku przedstawiono dwie bryły. Bryła I jest sześcianem o boku 5, a bryła II powstała z sześcianu o boku 5 przez usunięcie 6 sześcianów jednostkowych.
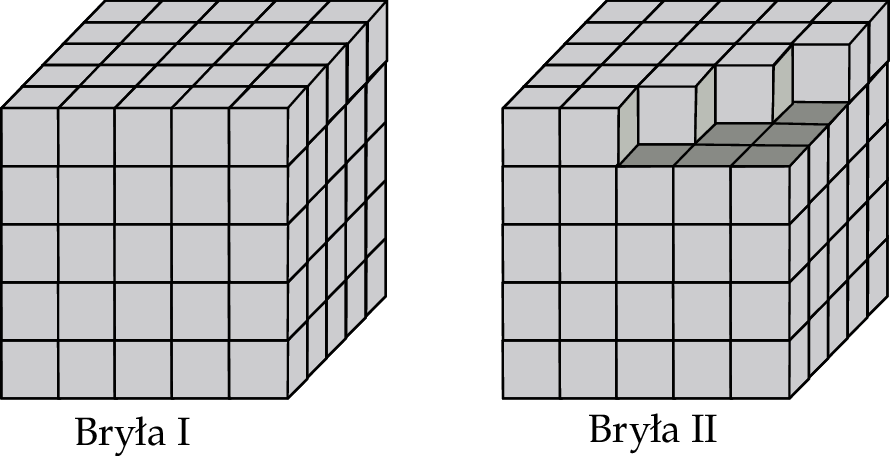
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Bryła II ma większe pole powierzchni niż bryła I. | P | F |
| Objętość bryły II przekracza 90% objętości bryły I | P | F |
W tabeli zapisano cztery liczby.
| I | 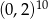 |
| II | 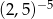 |
| III | 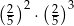 |
| IV | 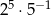 |
Liczba 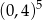 jest równa liczbom
jest równa liczbom
A) I i II B) I i III C) II i IV D) II i III E) III i IV
Graniastosłup prawidłowy czworokątny o krawędzi 4 cm i wysokości 3 cm przecięto płaszczyzną, która zawiera przekątne przeciwległych ścian bocznych. Jakie pole ma ten przekrój?
Oblicz promień okręgu opisanego na prostokącie, którego boki mają długości 6 cm i 8 cm.
Dane są liczby  i
i 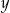 spełniające warunki:
spełniające warunki: 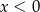 i
i 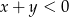 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczba 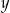 musi być ujemna. musi być ujemna. | P | F |
Liczby  i i 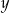 mogą być równe. mogą być równe. | P | F |
Suma liczb  i
i 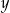 jest liczbą ujemną, a ich iloczyn jest liczbą dodatnią.
jest liczbą ujemną, a ich iloczyn jest liczbą dodatnią.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczby  i i 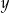 są różnych znaków. są różnych znaków. | P | F |
| Na osi liczbowej odległość każdej z tych liczb od 0 jest nie mniejsza od 1. | P | F |
Dane są liczby  i
i 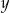 spełniające warunek:
spełniające warunek: 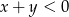 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczba 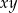 nie może być dodatnia. nie może być dodatnia. | P | F |
Liczba 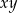 może być równa 0. może być równa 0. | P | F |
Suma liczb  i
i 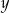 jest liczbą dodatnią, a ich iloczyn jest liczbą ujemną.
jest liczbą dodatnią, a ich iloczyn jest liczbą ujemną.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczby  i i 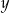 są różnych znaków. są różnych znaków. | P | F |
| Na osi liczbowej odległość każdej z tych liczb od zera jest taka sama. | P | F |
Dane są liczby  i
i 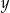 spełniające warunek:
spełniające warunek: 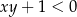 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczby  i i 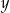 mają różne znaki. mają różne znaki. | P | F |
Suma liczb  i i 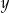 może być dodatnia. może być dodatnia. | P | F |
Kierowca samochodu dostawczego zanotował w tabeli informacje o 6 wyjazdach służbowych.
| L. p. | Liczba przejechanych kilometrów | Czas podróży |
| 1. | 170 | 2 h 50 min |
| 2. | 160 | 2 h 20 min |
| 3. | 120 | 2 h |
| 4. | 150 | 2 h 20 min |
| 5. | 310 | 5 h 10 min |
| 6. | 190 | 3 h 10 min |
Na podstawie informacji zawartych w powyższej tabeli wybierz zdanie prawdziwe.
A) Kierowca w ciągu jednego wyjazdu przejeżdżał średnio 180 km.
B) Trzy pierwsze wyjazdy trwały dłużej, niż trzy kolejne.
C) Podczas dwóch pierwszych wyjazdów kierowca przejechał 30% łącznej liczby kilometrów przejechanych podczas 6 wyjazdów.
D) Średnia prędkość podczas każdego z wyjazdów wyniosła 60 km/h.
W układzie współrzędnych zaznaczono wierzchołki sześciokąta 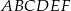 :
: 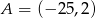 ,
, 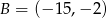 ,
, 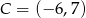 ,
, 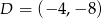 ,
, 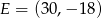 ,
, 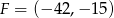 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Trzy wierzchołki sześciokąta 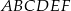 znajdują się w drugiej ćwiartce układu współrzędnych. znajdują się w drugiej ćwiartce układu współrzędnych. | P | F |
Dwa wierzchołki sześciokąta 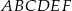 znajdują się w trzeciej ćwiartce układu współrzędnych. znajdują się w trzeciej ćwiartce układu współrzędnych. | P | F |
Dla każdej liczby rzeczywistej 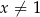 wyrażenie
wyrażenie 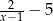 jest równe
jest równe
A) 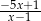 B)
B) 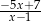 C)
C) 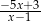 D)
D) 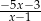
Dla każdej liczby rzeczywistej  różnej od 0 wartość wyrażenia
różnej od 0 wartość wyrażenia 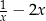 jest równa wartości wyrażenia
jest równa wartości wyrażenia
A)  B)
B) 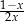 C)
C) 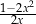 D)
D) 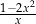
Dla każdej liczby rzeczywistej  różnej od 0 wartość wyrażenia
różnej od 0 wartość wyrażenia 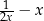 jest równa wartości wyrażenia
jest równa wartości wyrażenia
A)  B)
B) 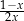 C)
C) 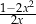 D)
D) 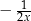
Dla każdej liczby rzeczywistej 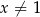 wyrażenie
wyrażenie 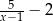 jest równe
jest równe
A) 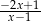 B)
B) 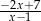 C)
C) 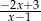 D)
D)