Średnia arytmetyczna cen sześciu akcji na giełdzie jest równa 500 zł. Za pięć z tych akcji zapłacono 2300 zł. Cena szóstej akcji jest równa
A) 400 zł B) 500 zł C) 600 zł D) 700 zł
/Szkoła podstawowa
Ala kupiła trzy zeszyty i blok rysunkowy. Średnia arytmetyczna cen tych czterech artykułów była równa 6 zł. Zeszyty kosztowały łącznie 15 zł. Ile kosztował blok rysunkowy?
A) 4 zł B) 5 zł C) 8 zł D) 9 zł
Kamil ma trzy siostry i jednego brata bliźniaka. Średnia wieku wszystkich dzieci w tej rodzinie jest równa 10,2 roku, a średnia wieku samych dziewcząt jest równa 7 lat. Ile lat ma Kamil?
A) 30 B) 17 C) 15 D) 21
Średnia arytmetyczna cen ośmiu akcji na giełdzie jest równa 600 zł. Za siedem z tych akcji zapłacono 4200 zł. Cena ósmej akcji jest równa
A) 400 zł B) 500 zł C) 600 zł D) 700 zł
Państwo Nowakowie mają trzy córki i jednego syna. Średnia wieku wszystkich dzieci państwa Nowaków jest równa 10 lat, a średnia wieku wszystkich córek jest równa 8 lat. Ile lat ma syn państwa Nowaków?
A) 9 B) 11 C) 12 D) 16
Średnia cena sześciu kartonów mleka po 3,2 zł za karton i dwóch identycznych pojemników śmietany wynosi 2,85 zł. Cena jednego pojemnika śmietany jest równa
A) 1,8 zł B) 3,6 zł C) 2 zł D) 2,4 zł
Średnia arytmetyczna cen dziewięciu akcji na giełdzie jest równa 680 zł. Za osiem z tych akcji zapłacono 5500 zł. Cena dziewiątej akcji jest równa
A) 660 zł B) 580 zł C) 620 zł D) 760 zł
Kasia kupiła cztery ołówki i długopis. Średnia arytmetyczna cen tych pięciu artykułów była równa 1,8 zł. Ołówki kosztowały łącznie 6 zł. Ile kosztował długopis?
A) 2,7 zł B) 1,5 zł C) 2 zł D) 3 zł
Dane jest wyrażenie 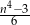 oraz liczby:
oraz liczby: 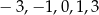 . Dla której z danych liczb wartość podanego wyrażenia jest najmniejsza?
. Dla której z danych liczb wartość podanego wyrażenia jest najmniejsza?
A) 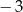 B)
B) 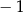 C) 0 D) 1 E) 3
C) 0 D) 1 E) 3
Dane jest wyrażenie 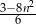 oraz liczby:
oraz liczby: 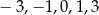 . Dla której z danych liczb wartość podanego wyrażenia jest największa?
. Dla której z danych liczb wartość podanego wyrażenia jest największa?
A) 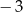 B)
B) 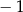 C) 0 D) 1 E) 3
C) 0 D) 1 E) 3
Cena lodówki wraz z 7% podatkiem VAT wynosi 1337 zł 50 gr. Oblicz ile wynosi podatek VAT.
Liczby:  ,
, 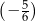 ,
, 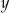 , są uporządkowane rosnąco. Liczba
, są uporządkowane rosnąco. Liczba 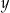 jest o 0,5 większa od
jest o 0,5 większa od 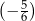 , a liczba
, a liczba 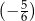 jest o 0,5 większa od liczby
jest o 0,5 większa od liczby  . Jakie wartości mają liczby
. Jakie wartości mają liczby  i
i 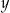 ?
?
A) 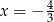 i
i 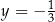 B)
B) 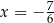 i
i 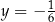
C) 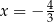 i
i 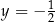 D)
D) 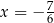 i
i 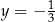
Liczby:  ,
, 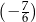 ,
, 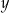 , są uporządkowane rosnąco. Liczba
, są uporządkowane rosnąco. Liczba 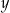 jest o 0,5 większa od
jest o 0,5 większa od 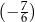 , a liczba
, a liczba 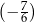 jest o 0,5 większa od liczby
jest o 0,5 większa od liczby  . Jakie wartości mają liczby
. Jakie wartości mają liczby  i
i 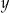 ?
?
A) 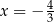 i
i 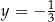 B)
B) 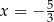 i
i 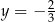
C) 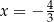 i
i 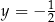 D)
D) 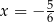 i
i 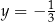
Na rysunku przedstawiony jest wykres funkcji liniowej 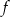 .
.
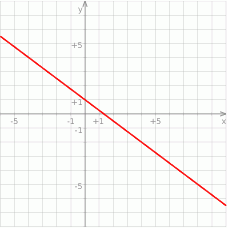
Funkcja 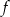 jest określona wzorem
jest określona wzorem
A) 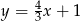 B)
B) 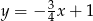 C)
C) 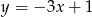 D)
D) 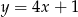
Na rysunku przedstawiony jest wykres funkcji liniowej 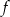 .
.
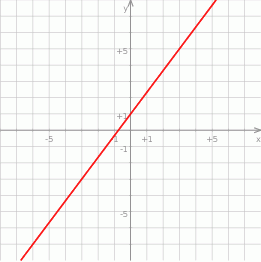
Funkcja 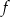 jest określona wzorem
jest określona wzorem
A) 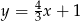 B)
B) 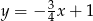 C)
C) 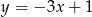 D)
D) 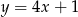
Wskaż wzór funkcji, której wykres przedstawiono na poniższym rysunku.
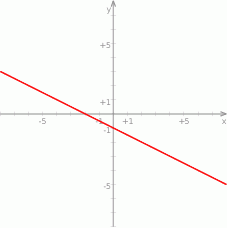
A) 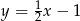 B)
B) 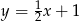 C)
C) 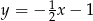 D)
D) 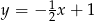
Wskaż wzór funkcji, której wykres przedstawiono na poniższym rysunku.
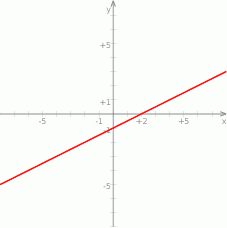
A) 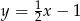 B)
B) 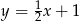 C)
C) 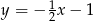 D)
D) 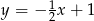
Na rysunku przedstawiony jest wykres funkcji liniowej 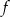 .
.
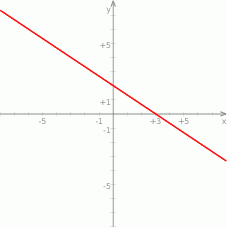
Funkcja 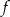 jest określona wzorem
jest określona wzorem
A) 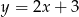 B)
B) 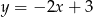 C)
C) 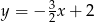 D)
D) 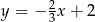
Na rysunku przedstawiony jest wykres funkcji liniowej  .
.
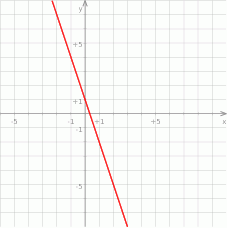
Funkcja 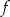 jest określona wzorem
jest określona wzorem
A) 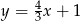 B)
B) 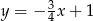 C)
C) 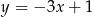 D)
D) 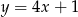
Na rysunku przedstawiony jest wykres funkcji liniowej 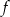 .
.
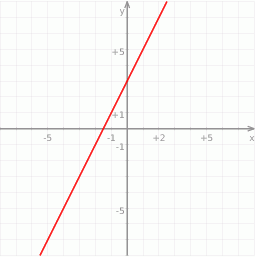
Funkcja 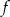 jest określona wzorem
jest określona wzorem
A) 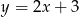 B)
B) 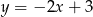 C)
C) 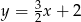 D)
D) 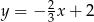
Na rysunku przedstawiony jest wykres funkcji liniowej 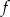 .
.
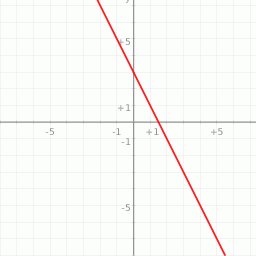
Funkcja 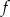 jest określona wzorem
jest określona wzorem
A) 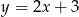 B)
B) 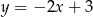 C)
C) 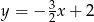 D)
D) 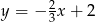
Na rysunku przedstawiono wykres funkcji  .
.
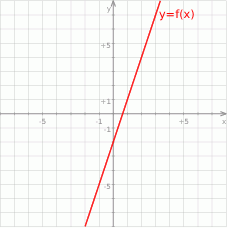
Wzór opisujący funkcję 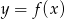 ma postać:
ma postać:
A) 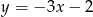 B)
B) 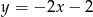 C)
C) 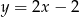 D)
D) 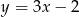
Wskaż wzór funkcji, której wykres przedstawiono na poniższym rysunku.
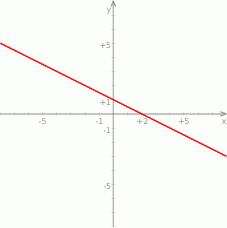
A) 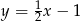 B)
B) 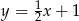 C)
C) 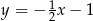 D)
D) 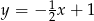
O ile procent sprzedaż samochodów przez firmę Bryka jest większy niż firmy Auto?
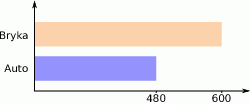
A) 20% B) 25% C) 80% D) 125%
O ile procent sprzedaż samochodów przez firmę Bryka jest większy niż firmy Auto?
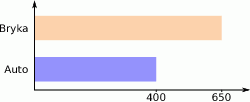
A) 50% B) 25% C) 80% D) 62,5%
O ile procent sprzedaż samochodów przez firmę Bryka jest większy niż firmy Auto?
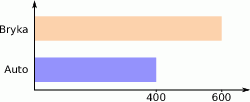
A) 20% B) 25% C) 50% D) 125%
Krem jest sprzedawany w trzech rodzajach pojemników. Każdy pojemnik ma kształt walca, którego wewnętrzne wymiary podane są na rysunku.
Objętość walca oblicza się ze wzoru 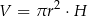 , gdzie
, gdzie  oznacza promień koła będącego podstawą walca,
oznacza promień koła będącego podstawą walca, 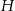 – wysokość walca.
– wysokość walca.
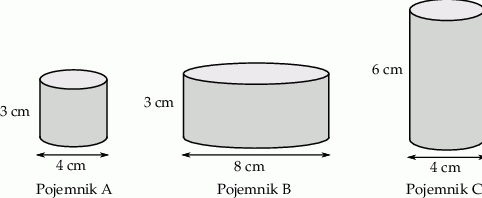
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
W pojemniku 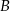 mieści się cztery razy więcej kremu niż w pojemniku mieści się cztery razy więcej kremu niż w pojemniku 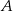 . . | P | F |
W pojemniku 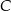 mieści się dwa razy mniej kremu niż w pojemniku mieści się dwa razy mniej kremu niż w pojemniku 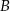 . . | P | F |
Na rysunku podano wymiary trzech prostopadłościennych pojemników.
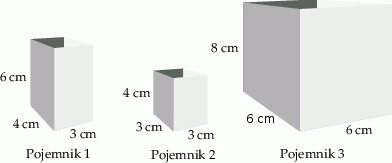
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Objętość pojemnika nr 2 jest dwa razy mniejsza od objętości pojemnika nr 1. | P | F |
| Objętość pojemnika nr 3 jest dwa razy większa od objętości pojemnika nr 1. | P | F |
Samochód przebył trasę łączącą miejscowości 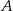 i
i 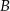 ze średnią prędkością
ze średnią prędkością 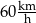 , a potem pokonał trasę między miejscowościami
, a potem pokonał trasę między miejscowościami 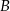 i
i 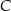 ze średnią prędkością
ze średnią prędkością 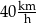 . Odległość między miastami
. Odległość między miastami 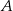 i
i 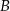 jest taka sama jak odległość między miastami
jest taka sama jak odległość między miastami 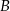 i
i 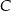 i wynosi 120 km.
i wynosi 120 km.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Średnia prędkość z jaką samochód przejechał całą trasę między 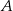 i i 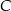 jest równa jest równa 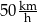 . . | P | F |
Gdyby średnia prędkość samochodu na trasie pomiędzy miastami 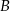 i i 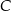 była równa była równa 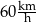 , to samochód pokonałby całą trasę między miastami , to samochód pokonałby całą trasę między miastami 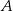 i i 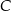 w czasie o godzinę krótszym. w czasie o godzinę krótszym. | P | F |
Tosia wybrała się na wycieczkę rowerową, której długość na mapie w skali 1:75 000 jest równa 22 cm. Tosia pokonała całą trasę w 90 minut. Rzeczywista długość trasy jaką pokonała Tosia jest równa A/B.
A) 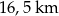 B)
B) 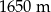
Średnia prędkość z jaką Tosia pokonała całą trasę wycieczki jest równa C/D.
C) 12 km/h D) 11 km/h
Z każdej z dwóch jednakowych kostek sześciennych wycięto sześcian i otrzymano bryły przedstawione na rysunku.
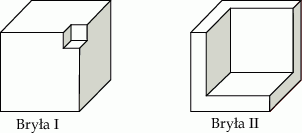
Czy całkowite pole powierzchni bryły I jest większe od całkowitego pola powierzchni bryły II? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
| Tak | Nie |
| ponieważ | |
| A) | z pierwszej kostki usunięto mniejszy sześcian niż z drugiej kostki. |
| B) | całkowite pole powierzchni każdej z otrzymanych brył jest równe całkowitemu polu powierzchni początkowej kostki. |
| C) | pole powierzchni „wnęki” w II bryle jest większe niż pole powierzchni „wnęki” w I bryle. |
Na rysunku przedstawiono sześcian 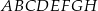 oraz trzy jego przekątne.
oraz trzy jego przekątne.
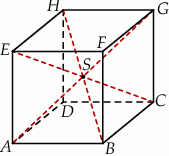
Czy kąty 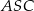 i
i 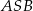 są równe? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
są równe? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
| Tak | Nie |
| ponieważ | |
| A) | wszystkie przekątne sześcianu mają tę samą długość. |
| B) | trójkąty 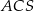 i i 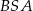 nie są przystające. nie są przystające. |
| C) | przekątne sześcianu są prostopadłe. |
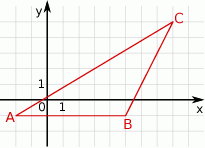
Oblicz pole trójkąta przedstawionego na rysunku.
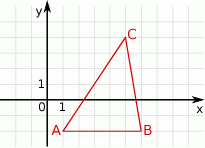
Oblicz pole trójkąta przedstawionego na rysunku.
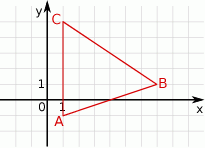
Oblicz pole trójkąta przedstawionego na rysunku.
Na most długości 200 m wjechała ciężarówka o długości 20 m. Ciężarówka porusza się z prędkością 36 km/h. Ile czasu upłynie od momentu wjazdu kabiny ciężarówki na most do momentu całkowitego zjechania ciężarówki z mostu?
A) 20 sekund B) 22 sekundy C) 200 sekund D) 24 sekundy
W układzie współrzędnych wyznaczono odcinek o końcach w punktach 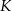 i
i 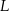 . Punkty te mają współrzędne
. Punkty te mają współrzędne 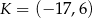 oraz
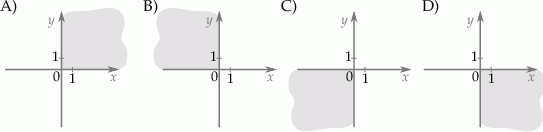
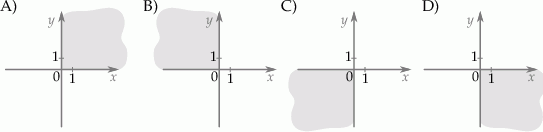
oraz 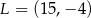 . Na którym rysunku zacieniowana część płaszczyzny zawiera środek odcinka
. Na którym rysunku zacieniowana część płaszczyzny zawiera środek odcinka 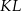 ?
?
W układzie współrzędnych wyznaczono odcinek o końcach w punktach 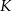 i
i 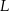 . Punkty te mają współrzędne
. Punkty te mają współrzędne 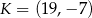 oraz
oraz 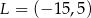 . Na którym rysunku zacieniowana część płaszczyzny zawiera środek odcinka
. Na którym rysunku zacieniowana część płaszczyzny zawiera środek odcinka 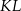 ?
?
Udowodnij, że w trójkącie równoramiennym środkowe poprowadzone do równych boków są równej długości.
Dana jest funkcja 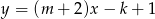 , gdzie
, gdzie  . Dla jakich wartości
. Dla jakich wartości  i
i 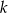 funkcja ta jest stała, a wykres jej jest prostą przecinającą oś
funkcja ta jest stała, a wykres jej jest prostą przecinającą oś 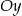 poniżej początku układu współrzędnych?
poniżej początku układu współrzędnych?
Która z nierówności jest prawdziwa?
A) 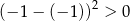 B)
B) 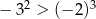 C)
C) 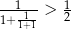 D)
D) 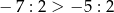
Na tablicy zapisano liczby 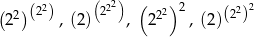 . Ile różnych liczb reprezentują te zapisy?
. Ile różnych liczb reprezentują te zapisy?
A) 4 B) 3 C) 2 D) 1
Zbiór punktów wspólnych kuli i prostej może być
A) zbiorem dwuelementowym B) zbiorem jednoelementowym C) okręgiem D) kołem
Zbiór punktów wspólnych kuli i płaszczyzny może być
A) zbiorem dwuelementowym B) okręgiem C) zbiorem jednoelementowym D) sferą
Adam ma narysować okrąg wpisany w trójkąt 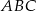 .
.
W punktach a), b) i c) zapisano czynności, które chłopiec musi wykonać:
- narysować prostą prostopadłą do jednego z boków trójkąta
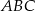 , przechodzącą przez punkt
, przechodzącą przez punkt 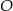 . Punkt przecięcia prostej prostopadłej i tego boku oznaczyć literą
. Punkt przecięcia prostej prostopadłej i tego boku oznaczyć literą 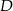 ,
, - narysować okrąg o środku w punkcie
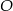 i promieniu
i promieniu 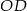 ,
, - narysować dwusieczne kątów wewnętrznych trójkąta
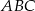 i ich punkt przecięcia oznaczyć literą
i ich punkt przecięcia oznaczyć literą 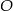 .
.
W jakiej kolejności Adam musi wykonać czynności opisane w punktach a), b) i c), aby rysunek był prawidłowy?
A) a, c, b B) c, a, b C) b, c, a D) c, b, a
Wykonano następującą konstrukcję.
1. Narysowano trójkąt 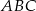 . 2. Wykreślono dwusieczne dwóch kątów wewnętrznych tego trójkąta i ich punkt przecięcia oznaczono literą
. 2. Wykreślono dwusieczne dwóch kątów wewnętrznych tego trójkąta i ich punkt przecięcia oznaczono literą 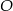 .
.
3. Poprowadzono prostą prostopadłą do boku 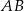 i przechodzącą przez punkt
i przechodzącą przez punkt 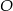 . Punkt przecięcia tej prostej i boku
. Punkt przecięcia tej prostej i boku 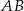 oznaczono literą
oznaczono literą 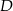 .
.
4. Narysowano okrąg o środku w punkcie 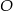 i promieniu
i promieniu 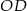 .
.
Skonstruowany w opisany powyżej sposób okrąg
A) przechodzi przez wszystkie wierzchołki tego trójkąta.
B) jest styczny do wszystkich boków tego trójkąta.
C) ma środek leżący na jednym z boków trójkąta.
D) przecina jeden z boków trójkąta w dwóch punktach.
W ramach prac konserwacyjnych opróżniono z wody zbiornik retencyjny. Wykres przedstawia zależność ilości pozostałej w zbiorniku wody (w 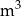 ) od czasu pracy pomp (w godzinach).
) od czasu pracy pomp (w godzinach).
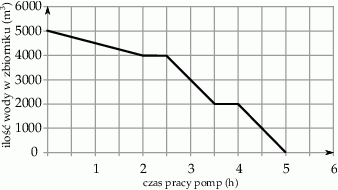
W trakcie wypompowywania wody nastąpiły dwie przerwy i w trakcie jednej z nich zwiększono wydajność pomp. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Łączny czas trwania przerw wyniósł 120 minut. | P | F |
| Wydajność pomp zwiększono w czasie pierwszej przerwy. | P | F |
W ramach prac konserwacyjnych opróżniono z wody zbiornik retencyjny. Wykres przedstawia zależność ilości pozostałej w zbiorniku wody (w 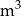 ) od czasu pracy pomp (w godzinach).
) od czasu pracy pomp (w godzinach).
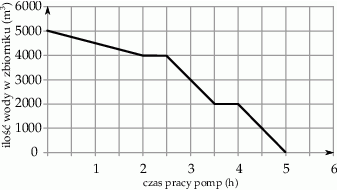
Jaka była średnia prędkość opróżniania całego zbiornika?
A) 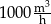 B)
B) 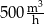 C)
C) 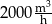 D)
D) 
W ramach prac konserwacyjnych opróżniono z wody zbiornik retencyjny. Wykres przedstawia zależność ilości pozostałej w zbiorniku wody (w 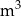 ) od czasu pracy pomp (w godzinach).
) od czasu pracy pomp (w godzinach).
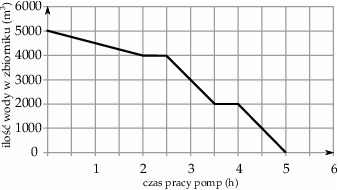
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Po 3,5 h wypompowano ze zbiornika połowę wody. | P | F |
Po 1 h wypompowano ze zbiornika 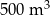 wody. wody. | P | F |

