/Studia/Analiza/Funkcje/Badanie funkcji/Granice

Zadanie nr 1849157

Dodaj do ulubionych
Dodaj do rozwiązanych

Zbadać czy istnieje granica 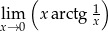( 1) lixm→0 x arctg x .

Rozwiązanie

Sposób I

Ponieważ funkcja 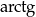arctg jest ograniczona przez 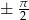± π- 2 , mamy

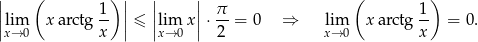
| ( ) | | | ( ) | 1 | | | π 1 ||lim xarctg -- || ≤ ||lim x|| ⋅--= 0 ⇒ lim x arctg -- = 0. x→ 0 x x→ 0 2 x→0 x

To samo można oczywiście też zapisać przy pomocy twierdzenia o trzech funkcjach.

Sposób II

Policzmy granice jednostronne.

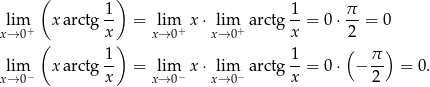
( ) lim xa rctg 1- = lim x⋅ lim arctg 1-= 0 ⋅ π = 0 x→ 0+ x x→ 0+ x→ 0+ x 2 ( 1) 1 ( π ) lim− xa rctg -- = lim − x⋅ lim− arctg --= 0 ⋅ − -- = 0. x→ 0 x x→ 0 x→ 0 x 2

Ponieważ granice te są równe, 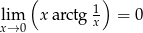( ) lim xa rctg 1 = 0 x→ 0 x .  
Odpowiedź: 0

Wersja PDF