Zadanie nr 3067573
Oblicz granicę 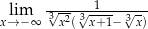 .
.
Rozwiązanie
Mnożymy licznik i mianownik funkcji w granicy przez
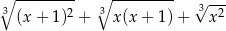
tak, aby skorzystać ze wzoru
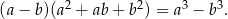
Mamy zatem
![∘ --------- ∘ --------- √ --- 1 3 (x+ 1)2 + 3 x(x + 1) + 3x 2 lim √3---√3---------√--- = lim 3√----3√---------√----∘------------∘-------------√3----= x→ −∞ x2( x + 1− 3 x) x→ −∞ x2( x + 1 − 3x)( 3 (x+ 1)2 + 3 x(x + 1) + x2) 3∘ -------2- 3∘ --------- √3--2 = lim --(√x-+[1)(√+----x()x-+-1(-)+)-]x---= x→ −∞ 3 x2 3 x+ 1 3 − √3x 3 ∘ --------- ∘ --------- √ --- 3 (x + 1)2 + 3 x(x + 1 )+ 3x 2 = lim -------------√3-----------------= x→ −∞ [ ∘ --------- ∘x2--------- ] 3 (x + 1)2 3 x(x + 1) = lim -----2---+ ----2----+ 1 = x→ −∞ x x ⌊ ∘ (-------)2- ∘ ------ ⌋ ⌈ 3 1- 1- ⌉ = xl→im−∞ 1 + x + 1 + x + 1 = 3](https://img.zadania.info/zad/3067573/HzadR2x.gif)
Odpowiedź: 3
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz granicę 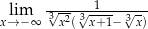 .
.
Mnożymy licznik i mianownik funkcji w granicy przez
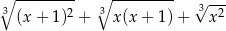
tak, aby skorzystać ze wzoru
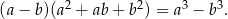
Mamy zatem
![∘ --------- ∘ --------- √ --- 1 3 (x+ 1)2 + 3 x(x + 1) + 3x 2 lim √3---√3---------√--- = lim 3√----3√---------√----∘------------∘-------------√3----= x→ −∞ x2( x + 1− 3 x) x→ −∞ x2( x + 1 − 3x)( 3 (x+ 1)2 + 3 x(x + 1) + x2) 3∘ -------2- 3∘ --------- √3--2 = lim --(√x-+[1)(√+----x()x-+-1(-)+)-]x---= x→ −∞ 3 x2 3 x+ 1 3 − √3x 3 ∘ --------- ∘ --------- √ --- 3 (x + 1)2 + 3 x(x + 1 )+ 3x 2 = lim -------------√3-----------------= x→ −∞ [ ∘ --------- ∘x2--------- ] 3 (x + 1)2 3 x(x + 1) = lim -----2---+ ----2----+ 1 = x→ −∞ x x ⌊ ∘ (-------)2- ∘ ------ ⌋ ⌈ 3 1- 1- ⌉ = xl→im−∞ 1 + x + 1 + x + 1 = 3](https://img.zadania.info/zad/3067573/HzadR2x.gif)
Odpowiedź: 3
