Zadanie nr 3096129
Oblicz granicę jednostronną funkcji 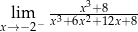 .
.
Rozwiązanie
Zauważmy, że w mianowniku danego wyrażenia mamy pełen sześcian
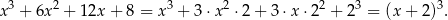
W liczniku mamy za to sumę sześcianów
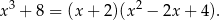
Interesująca nas granica jest więc równa
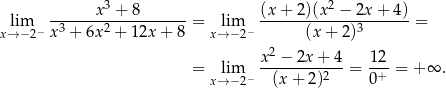
Odpowiedź: 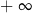
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz granicę jednostronną funkcji 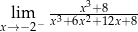 .
.
Zauważmy, że w mianowniku danego wyrażenia mamy pełen sześcian
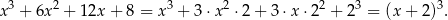
W liczniku mamy za to sumę sześcianów
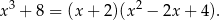
Interesująca nas granica jest więc równa
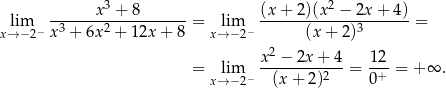
Odpowiedź: