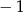Zadanie nr 4191611
Oblicz granicę 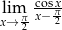 .
.
Rozwiązanie
Sposób I
Korzystamy z reguły de l’Hospitala (mamy  ).
).
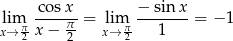
Sposób II
Tym razem skorzystamy z granicy 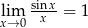 i ze wzoru redukcyjnego.
i ze wzoru redukcyjnego.
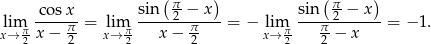
Odpowiedź: 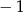
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz granicę 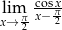 .
.
Sposób I
Korzystamy z reguły de l’Hospitala (mamy  ).
).
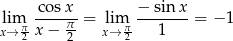
Sposób II
Tym razem skorzystamy z granicy 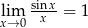 i ze wzoru redukcyjnego.
i ze wzoru redukcyjnego.
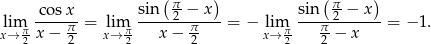
Odpowiedź: