Oblicz z definicji pochodną funkcji 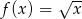 .
.
/Studia/Analiza/Funkcje/Badanie funkcji/Pochodne
Oblicz z definicji pochodną funkcji 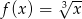 .
.
Oblicz z definicji pochodną funkcji 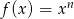 , gdzie
, gdzie 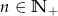 .
.
Wyznacz te argumenty, dla których funkcja 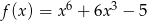 osiąga wartość najmniejszą.
osiąga wartość najmniejszą.
Oblicz pochodną funkcji 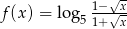 .
.
Oblicz pochodną funkcji 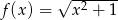 .
.
Wyznacz przedziały monotoniczności i ekstrema lokalne funkcji 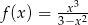 .
.
Wyznacz punkty przegięcia wykresu funkcji 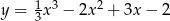 .
.
Oblicz pochodną funkcji 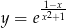 .
.
Wyznacz ekstrema lokalne funkcji 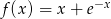 .
.
Wyznacz ekstrema lokalne funkcji 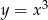 .
.
Wyznacz ekstrema lokalne funkcji 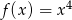 .
.
Wyznacz wszystkie wartości parametru  , dla których prosta
, dla których prosta 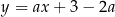 jest styczna do wykresu funkcji
jest styczna do wykresu funkcji 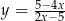 w punkcie o drugiej współrzędnej równej 3.
w punkcie o drugiej współrzędnej równej 3.
Funkcja 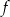 określona jest wzorem
określona jest wzorem 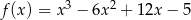 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równania tych stycznych do wykresu funkcji
. Wyznacz równania tych stycznych do wykresu funkcji 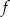 , które przechodzą przez punkt
, które przechodzą przez punkt 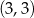 .
.
Wyznacz maksymalne przedziały monotoniczności funkcji 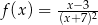 .
.
Prosta postaci 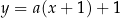 jest styczna do wykresu funkcji
jest styczna do wykresu funkcji 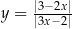 w punkcie
w punkcie 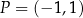 . Oblicz
. Oblicz  .
.
Dana jest funkcja 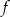 określona wzorem
określona wzorem 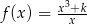 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 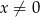 . Oblicz wartość
. Oblicz wartość 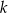 , dla której prosta o równaniu
, dla której prosta o równaniu 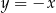 jest styczna do wykresu funkcji
jest styczna do wykresu funkcji 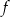 .
.
Dana jest funkcja 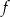 określona wzorem
określona wzorem 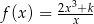 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 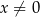 . Oblicz wartość
. Oblicz wartość 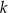 , dla której prosta o równaniu
, dla której prosta o równaniu 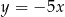 jest styczna do wykresu funkcji
jest styczna do wykresu funkcji 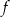 .
.
Zbadaj wypukłość funkcji 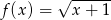 .
.
Wyznacz maksymalne przedziały monotoniczności funkcji 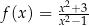 .
.
Dana jest funkcja kwadratowa 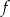 określona wzorem
określona wzorem 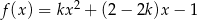 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  i
i 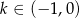 . Wyznacz równania dwóch prostopadłych stycznych do wykresu funkcji
. Wyznacz równania dwóch prostopadłych stycznych do wykresu funkcji 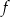 poprowadzonych w punktach, których pierwsze współrzędne różnią się o 2, jeżeli wiadomo, że funkcja
poprowadzonych w punktach, których pierwsze współrzędne różnią się o 2, jeżeli wiadomo, że funkcja 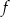 ma maksimum lokalne równe
ma maksimum lokalne równe  .
.
Punkt 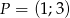 należy do wykresu funkcji
należy do wykresu funkcji 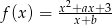 , gdzie
, gdzie 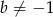 . Styczna do wykresu danej funkcji, poprowadzona w punkcie
. Styczna do wykresu danej funkcji, poprowadzona w punkcie 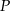 , jest prostopadła do prostej o równaniu
, jest prostopadła do prostej o równaniu 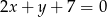 . Oblicz współczynniki
. Oblicz współczynniki  i
i 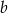 oraz napisz równanie tej stycznej.
oraz napisz równanie tej stycznej.
Punkt 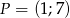 należy do wykresu funkcji
należy do wykresu funkcji 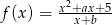 , gdzie
, gdzie 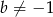 . Styczna do wykresu danej funkcji, poprowadzona w punkcie
. Styczna do wykresu danej funkcji, poprowadzona w punkcie 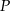 , jest prostopadła do prostej o równaniu
, jest prostopadła do prostej o równaniu 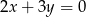 . Oblicz współczynniki
. Oblicz współczynniki  i
i 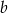 oraz napisz równanie tej stycznej.
oraz napisz równanie tej stycznej.
Wyznacz równanie stycznej do wykresu funkcji 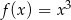 , która przecina oś
, która przecina oś 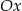 w jednym punkcie:
w jednym punkcie: 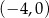 .
.

