/Studia/Analiza/Funkcje/Badanie funkcji/Pochodne

Zadanie nr 4279814

Dodaj do ulubionych
Dodaj do rozwiązanych

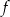Funkcja f jest określona wzorem 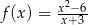x2−6 f(x ) = x+ 3 dla każdej liczby rzeczywistej 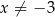x ⁄= − 3 . Wyznacz równanie stycznej do wykresu tej funkcji w punkcie ( ) P = 3, 1 2 .

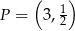Rozwiązanie

Będziemy korzystać z tego, że współczynnik kierunkowy stycznej do wykresu funkcji 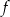f w punkcie 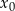x0 jest równy pochodnej 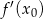f′(x0) w tym punkcie. Liczymy pochodną

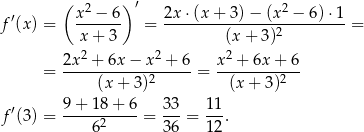
( )′ ′ x2-−-6- 2x-⋅(x-+-3-)−-(x-2 −-6)-⋅1 f (x) = x+ 3 = (x+ 3)2 = 2x-2 +-6x−--x2-+-6 x2 +-6x+--6- = (x + 3)2 = (x + 3)2 f′(3) = 9-+-1-8+--6 = 33-= 11-. 62 36 12

Sposób I

Korzystamy ze wzoru

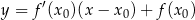
′ y = f (x0)(x − x0) + f(x0)

na styczną do wykresu 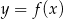y = f(x) w punkcie 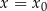x = x0 . Mamy zatem

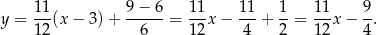
11 9 − 6 11 11 1 11 9 y = --(x − 3) + ------= ---x− ---+ --= ---x− -. 12 6 12 4 2 12 4

Sposób II

Wiemy, że styczna jest postaci 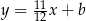y = 11x + b 12 . Współczynnik 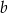b wyliczamy z tego, że ma ona przechodzić przez punkt ( 1) 3,2 .

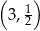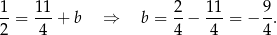
1 11 2 11 9 --= ---+ b ⇒ b = --− ---= − --. 2 4 4 4 4

Styczna ma więc równanie 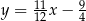11 9 y = 12x − 4 .

Na koniec obrazek dla ciekawskich.

PIC

 
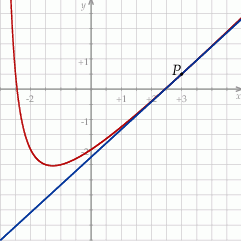
Odpowiedź: y = 1112x− 94

Wersja PDF