/Studia/Analiza/Funkcje/Badanie funkcji/Pochodne

Zadanie nr 4504045

Dodaj do ulubionych
Dodaj do rozwiązanych

Zbadaj wypukłość funkcji 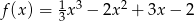1 3 2 f (x) = 3x − 2x + 3x− 2 .

Rozwiązanie

Liczymy drugą pochodną

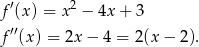
′ 2 f (x ) = x − 4x + 3 f ′′(x) = 2x − 4 = 2(x − 2).

Widać, że druga pochodna jest dodatnia dla 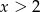x > 2 i ujemna dla 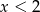x < 2 . To oznacza, że funkcja jest wypukła na przedziale 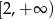[2,+ ∞ ) i wklęsła na przedziale (− ∞ ,2] .

Na koniec obrazek.

PIC

 
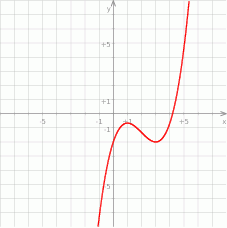
Odpowiedź: Wypukła na 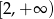[2,+ ∞ ) , wklęsła na (− ∞ ,2] .

Wersja PDF