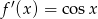Zadanie nr 5325630
Oblicz z definicji pochodną funkcji 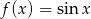 .
.
Rozwiązanie
Skorzystamy z granicy
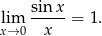
oraz z tożsamości trygonometrycznej
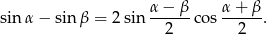
Liczymy pochodną w punkcie 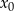 .
.
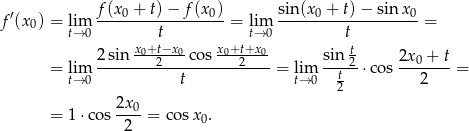
Odpowiedź: 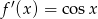
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz z definicji pochodną funkcji 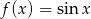 .
.
Skorzystamy z granicy
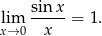
oraz z tożsamości trygonometrycznej
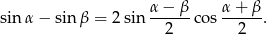
Liczymy pochodną w punkcie  .
.
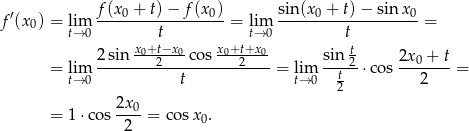
Odpowiedź: