/Studia/Analiza/Funkcje/Badanie funkcji/Pochodne

Zadanie nr 6583239

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz punkty przegięcia wykresu funkcji 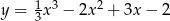1 3 2 y = 3x − 2x + 3x− 2 .

Rozwiązanie

Liczymy drugą pochodną

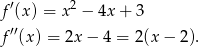
′ 2 f (x ) = x − 4x + 3 f ′′(x) = 2x − 4 = 2(x − 2).

Widać, że druga pochodna zmienia znak przechodząc przez punkt 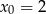x0 = 2 . Zatem punkt ten jest punktem przegięcia.

Na koniec obrazek.

PIC

 
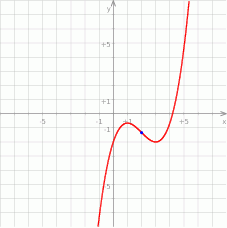
Odpowiedź: Punkt przegięcia: 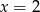x = 2 .

Wersja PDF