Zadanie nr 6888060
Wyznacz maksymalne przedziały monotoniczności funkcji 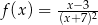 .
.
Rozwiązanie
Korzystamy ze wzoru na pochodną ilorazu
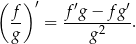
Liczymy
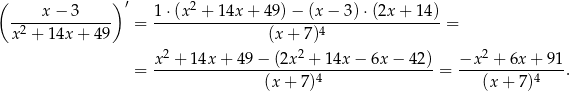
Aby ustalić jaki jest znak licznika otrzymanego wyrażenia wyznaczamy jego pierwiastki.
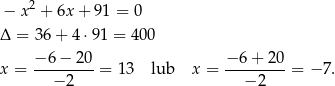
Mamy zatem
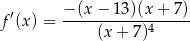
Widzimy teraz, że 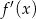 jest dodatnia dla
jest dodatnia dla 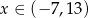 i ujemna dla
i ujemna dla 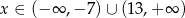 . To oznacza, że
. To oznacza, że 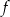 rośnie w przedziale
rośnie w przedziale 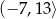 i maleje w każdym z przedziałów:
i maleje w każdym z przedziałów: 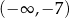 i
i 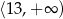 .
.
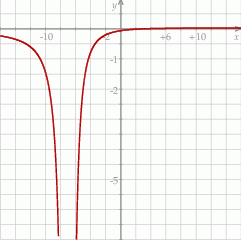
Na koniec dla ciekawskich wykres funkcji  .
.
Odpowiedź: Rosnąca w 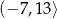 , malejąca w
, malejąca w 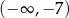 i
i 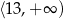 .
.

