/Studia/Analiza/Funkcje/Badanie funkcji/Pochodne

Zadanie nr 7331769

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz wszystkie wartości parametru 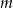m , dla których prosta 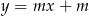y = mx + m jest styczna do wykresu funkcji y = 1x3 .

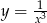Rozwiązanie

Liczymy pochodną danej funkcji

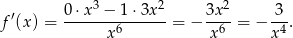
3 2 2 f′(x) = 0⋅x--−-1-⋅3x--= − 3x--= − 3-. x 6 x6 x4

Styczna do wykresu funkcji 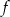f w punkcie 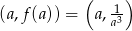( 1-) (a,f(a)) = a,a3 ma więc współczynnik kierunkowy 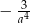− 3- a4 i równanie postaci 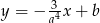y = − -3x + b a4 . Współczynnik 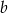b wyznaczamy podstawiając współrzędne punktu ( ) a, 1a3 .

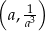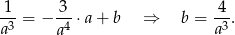
-1-= − 3-⋅ a+ b ⇒ b = -4-. a3 a4 a3

Styczna do wykresu funkcji 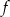f ma więc postać

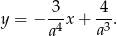
3 4 y = − --x+ --. a4 a3

Musimy więc wyznaczyć 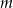m takie, że

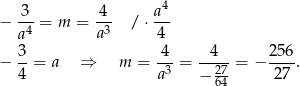
4 − -3-= m = 4-- / ⋅ a-- a4 a3 4 3- -4- -4--- 256- − 4 = a ⇒ m = a3 = − 27 = − 27 . 64

Jest więc jedna prosta spełniająca warunki zadania:

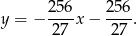
y = − 256-x− 256-. 27 27

Na koniec obrazek dla ciekawskich.

PIC

 
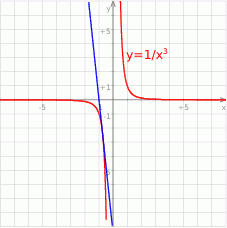
Odpowiedź: m = − 25267

Wersja PDF