Każdą ścianę sześciennej kostki do gry malujemy jednym z dwóch ustalonych kolorów (nie zamalowując oczek). Ile różnych dwukolorowych kostek można w ten sposób otrzymać?
A) 64 B) 62 C) 48 D) 36 E) 24
/Konkursy/Zadania testowe/Kombinatoryka
Jaka jest minimalna liczba punktów, które należy usunąć z rysunku, aby żadne trzy punkty spośród pozostałych nie leżały na jednej prostej?
A) 3 B) 4 C) 2 D) 7 E) 1
Ile jest liczb dziesięciocyfrowych, które można napisać przy użyciu cyfr 1,2 i 3 tak, aby każde dwie sąsiednie cyfry w ich zapisach różniły się o jeden?
A) 16 B) 32 C) 64 D) 80 E) 100
Jakim procentem liczby elementów zboru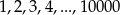 
jest liczba tych jego elementów, które są kwadratami liczb naturalnych?
A) 1% B) 5% C) 10% D) 50% E) 0,1%
Ile jest liczb 2008–cyfrowych, których każde dwie kolejne cyfry tworzą liczbę podzielną przez 17 lub przez 23?
A) 5 B) 6 C) 7 D) 9 E) Więcej niż 9
Każda z liczb 257,338 ma tę własność, że jeśli jej cyfry zapiszemy w odwrotnej kolejności, to otrzymamy liczbę od niej większą. Ile jest wszystkich liczb trzycyfrowych o tej własności?
A) 124 B) 252 C) 280 D) 288 E) 360
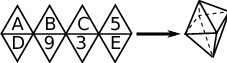
Z siatki składającej się z 8 trójkątów równobocznych można skleić ośmiościan foremny, jak na rysunku obok. Aby powstał ośmiościan magiczny, trzeba zamienić litery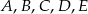 
na liczby 2,4,6,7,8 (każdą literę na inną liczbę) w ten sposób, by sumy liczb na czterech ścianach przy każdym wierzchołku były sobie równe. Ile wówczas będzie równe 
?
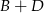A) 6 B) 7 C) 8 D) 9 E) 10
Ile dróg prowadzi od górnego do dolnego końca przeciwprostokątnej dużego trójkąta, jeśli wolno poruszać się po bokach małych trójkątów w sposób przedstawiony na rysunku
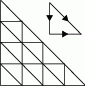
A) 16 B) 27 C) 64 D) 90 E) 111
Drewniany sześcian wymiaru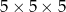 
został zbudowany poprzez sklejenie ze sobą 
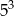sześcianów jednostkowych. Kleofas sfotografował ten sześcian w taki sposób, aby na zdjęciu widać było największą możliwą liczbę sześcianów jednostkowych. Ile sześcianów jednostkowych było widocznych na zdjęciu wykonanym przez Kleofasa.
A) 75 B) 74 C) 60 D) 61 E) 62
Pięć liczb całkowitych rozmieszczono na okręgu. Okazało się, że dla każdych dwóch sąsiadujących ze sobą liczb, ani ich suma, ani suma pozostałych trzech nie jest podzielna przez 3. Ile wśród tych pięciu liczb jest podzielnych przez 3?
A) 0 B) 1 C) 2 D) 3 E) Nie można tego wyznaczyć
Ile jest możliwych dróg o minimalnej liczbie ruchów, prowadzących z lewego górnego rogu diagramu do jego prawego dolnego rogu, które może wykonać król szachowy (w jednym ruchu król może przesunąć się na dowolne sąsiednie pole stykające się bokiem lub wierzchołkiem)?
A) 1 B) 4 C) 3 D) 20 E) 2
Pięcioosobowe zespoły z dwóch szkół mają rozegrać pomiędzy sobą zawody w tenisie stołowym par. Każda para zawodników jednej szkoły musi rozegrać z każdą parą zawodników z drugiej szkoły dokładnie jedno spotkanie. W ilu spotkaniach zagra każdy z 10 zawodników?
A) 10 B) 20 C) 30 D) 40 E) 50
W każde pole tablicy o wymiarach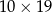 
wpisujemy 0 lub 1. Wyznaczamy sumy liczb stojących w każdym wierszu i w każdej kolumnie. Największa możliwa liczba różnych sum, które można w ten sposób otrzymać, jest równa
A) 9 B) 10 C) 15 D) 19 E) 29
Planujemy pokolorować kratki kwadratu, używając kolorów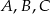 
i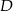 
w taki sposób, by żadne dwie kratki o wspólnym boku lub wierzchołku nie były pokolorowane tym samym kolorem. Pewne kratki są już pokolorowane (patrz rysunek).
Jakie są możliwe pokolorowania kratki zacieniowanej?
A) Tylko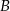 
. B) Tylko 
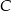. C) Tylko 
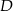. D) Albo 
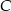, albo 
.
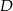E) Kwadratu tego nie można tak pokolorować.
Z jabłek, śliwek, pomarańczy i bananów układamy na półce kompozycje, kładąc kolejno owoc za owocem. Kompozycja jest kompletna, gdy bezpośrednio za owocem dowolnego rodzaju przynajmniej raz leży owoc każdego innego rodzaju. Z ilu owoców składa się najmniej liczna kompletna kompozycja owoców?
A) 13 B) 8 C) 16 D) 4 E) 12
W kwadraciki tablicy 3x3 wpisane są liczby naturalne (rysunek obok). Ada wykreśliła z tablicy 4 liczby, a następnie Maria wykreśliła z pozostałych także 4 liczby. Okazało się, że suma liczb skreślonych przez Adę jest trzy razy większa od sumy liczb skreślonych przez Marię. Jaka liczba pozostała nie skreślona ?
A) 4 B) 7 C) 14 D) 23 E) 24
Cztery liczby, wśród nich 2, 3, 4, rozmieszczono w polach tabeli. Wiadomo, że suma liczb w pierwszym wierszu jest równa 9, a suma liczb w drugim wierszu jest równa 6. Czwarta liczbą jest
A) 4 B) 5 C) 6 D) 7 E) 8
Pociąg składa się z lokomotywy (na początku składu) i pięciu wagonów oznaczonych numerami: I,II,III,IV,V. Na ile sposobów można zestawić skład tego pociągu tak, aby wagon I był bliżej lokomotywy niż wagon II?
A) 120 B) 60 C) 48 D) 30 E) 10
W spotkaniu piłkarskim drużyna gospodarzy jako pierwsza objęła prowadzenie i nie straciła go do końca meczu. Mecz zakończył się zwycięstwem gospodarzy w stosunku 5:4. Na ile sposobów mogły padać bramki w tym meczu?
A) 17 B) 13 C) 20 D) 14 E) 9
Spośród liczb wpisanych do tablicy obok wybieramy trzy liczby tak, aby żadne dwie z nich nie leżały w tym samym wierszu ani w tej samej kolumnie. Największa suma liczb w tak wybranych trójkach jest równa
A) 12 B) 15 C) 18 D) 21 E) 24
