Ile liczb trzycyfrowych ma sumę cyfr równą 4?
A) 11 B) 6 C) 9 D) 8 E) 10
/Konkursy/Zadania testowe/Kombinatoryka
Dane są dwa zbiory liczb czterocyfrowych: zbiór 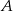 tych liczb, których iloczyn cyfr jest równy 25, oraz zbiór
tych liczb, których iloczyn cyfr jest równy 25, oraz zbiór 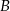 tych liczb, których iloczyn cyfr jest równy 15. Do którego zbioru należy więcej liczb i ile razy więcej liczb jest w tym zbiorze?
tych liczb, których iloczyn cyfr jest równy 15. Do którego zbioru należy więcej liczb i ile razy więcej liczb jest w tym zbiorze?
A) Zbiór 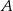 ma
ma  razy więcej elementów niż zbiór
razy więcej elementów niż zbiór 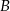 .
.
B) Zbiór 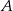 ma 2 razy więcej elementów niż zbiór
ma 2 razy więcej elementów niż zbiór 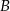 .
.
C) Zbiór 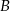 ma
ma 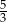 razy więcej elementów niż zbiór
razy więcej elementów niż zbiór 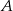 .
.
D) Zbiór 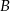 ma 2 razy więcej elementów niż zbiór
ma 2 razy więcej elementów niż zbiór 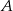 .
.
E) Oba zbiory mają po tyle samo elemantów
Do narysowania przedstawionej na rysunku tablicy zawierającej 12 komórek użyto 5 prostych poziomych i 4 pionowych. Jeżeli użyjemy 6 prostych poziomych i 3 pionowych, to otrzymamy tablice o 10 komórkach. Jaką największą liczbę komórek można otrzymać, używając do narysowania tablicy 15 prostych?

A) 56 B) 27 C) 32 D) 40 E) 42
Na różnych prostych równoległych  i
i 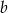 obrano 6 punktów: 4 punkty na prostej
obrano 6 punktów: 4 punkty na prostej  i 2 punkty na prostej
i 2 punkty na prostej 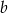 . Ile jest trójkątów, których wszystkie wierzchołki są w wybranych punktach?
. Ile jest trójkątów, których wszystkie wierzchołki są w wybranych punktach?
A) 6 B) 8 C) 12 D) 16 E) 18
W polach szachownicy 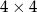 chcemy umieścić pionki w taki sposób, że liczby pionków w każdym wierszu i w każdej kolumnie szachownicy będą różne (w jednym polu można umieścić jeden lub więcej pionków, a także można pozostawić pole puste). Jaka jest minimalna liczba pionków, które można w taki sposób rozmieścić na szachownicy?
chcemy umieścić pionki w taki sposób, że liczby pionków w każdym wierszu i w każdej kolumnie szachownicy będą różne (w jednym polu można umieścić jeden lub więcej pionków, a także można pozostawić pole puste). Jaka jest minimalna liczba pionków, które można w taki sposób rozmieścić na szachownicy?
A) 7 B) 10 C) 14 D) 18 E) 28
Czworo przyjaciół zamierza na przyjęciu dać sobie nawzajem prezenty w taki sposób, że każdy da tylko jednej osobie prezent, i każdy otrzyma prezent tylko od jednej osoby (oczywiście nikt nie daje prezentu sobie). Na ile sposobów można to zrobić?
A) 9 B) 10 C) 12 D) 16 E) 24
Dana jest kula o promieniu 3 i o środku w początku układu współrzędnych. Ile punktów na powierzchni tej kuli ma wszystkie współrzędne całkowite?
A) 30 B) 24 C) 12 D) 6 E) 3
Na okręgu rozmieszczono liczby: 1,2,3. Pomiędzy każde dwie sąsiednie liczby wpisano ich sumy, otrzymując na okręgu sześć liczb 1,3,2,5,3,4. Operację wpisywania sum liczb sąsiednich powtórzono jeszcze trzy razy. W rezultacie otrzymano na okręgu 48 liczb. Ile wynosi ich suma?
A) 162 B) 1458 C) 486 D) 144 E) 210
Jeżeli każdy z wierzchołków 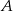 i
i 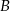 trójkąta
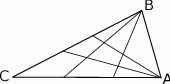
trójkąta 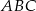 połączymy odcinkami z dwoma różnymi punktami leżącymi na przeciwległym boku, to odcinki te podzielą ten trójkąt na dziewięć części (patrz rysunek). Na ile części zostanie podzielony trójkąt, jeżeli każdy z wierzchołków
połączymy odcinkami z dwoma różnymi punktami leżącymi na przeciwległym boku, to odcinki te podzielą ten trójkąt na dziewięć części (patrz rysunek). Na ile części zostanie podzielony trójkąt, jeżeli każdy z wierzchołków 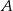 i
i 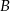 połączymy odcinkami z czterema punktami (różnymi od wierzchołków) leżącymi na przeciwległym do nich boku?
połączymy odcinkami z czterema punktami (różnymi od wierzchołków) leżącymi na przeciwległym do nich boku?
A) 16 B) 25 C) 36 D) 42 E) 49
Ile kwadratów można narysować, łącząc odcinkami kropki na rysunku obok?

A) 2 B) 3 C) 4 D) 5 E) 6
Kolejne wyrazy ciągu 1,2,3,4,5,6,7,8,9,1,2,3,4,5,6,7,8,9... wpisujemy spiralnie w kratki nieskończonego diagramu, tak jak na rysunku obok. Jaką liczbę wpiszemy w setnej kratce ponad kratką zacieniowaną?
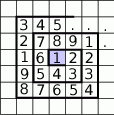
A) 8 B) 5 C) 6 D) 1 E) 3
Pięcioro przyjaciół zamierza na przyjęciu dać sobie nawzajem prezenty w taki sposób, że każdy da tylko jednej osobie prezent, i każdy otrzyma prezent tylko od jednej osoby (oczywiście nikt nie daje prezentu sobie). Na ile sposobów można to zrobić?
A) 5 B) 10 C) 44 D) 50 E) 120
Ile nieujemnych liczb całkowitych mniejszych od 100 można otrzymać jako sumę dziewięciu kolejnych liczb całkowitych?
A) 13 B) 12 C) 11 D) 10 E) 9
Zepsuty kalkulator nie wyświetla cyfry 1. Na przykład, jeśli wpiszemy liczbę 3131, to pokazuje on liczbę 33 bez żadnych odstępów między cyframi. Michał napisał na tym kalkulatorze pewną liczbę sześciocyfrową i na wyświetlaczu kalkulatora pojawiła się liczba 2007. Dla ilu liczb mogło się tak zdarzyć?
A) 12 B) 13 C) 14 D) 15 E) 16
Halina narysowała kwadrat o wymiarach 5x5 i zaznaczyła na rysunku środki kwadracików jednostkowych. Następnie umieściła przeszkody (pogrubione linie – patrz rysunek) i badała, na ile sposobów można przejść od punktu 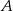 do punktu
do punktu 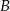 najkrótszą drogą, idąc pionowymi lub poziomymi odcinkami od środka kwadracika do środka kwadracika i omijając przeszkody. Ile jest takich najkrótszych dróg?
najkrótszą drogą, idąc pionowymi lub poziomymi odcinkami od środka kwadracika do środka kwadracika i omijając przeszkody. Ile jest takich najkrótszych dróg?

A) 6 B) 8 C) 9 D) 11 E) 12
Powierzchnia bryły narysowanej obok składa się z 6 ścian trójkątnych. W każdym wierzchołku bryły umieszczono liczbę tak, by sumy liczb umieszczonych w wierzchołkach danej ściany były jednakowe dla wszystkich ścian. Dwie liczby 3 i 6 są zaznaczone na rysunku. Ile wynosi suma wszystkich liczb umieszczonych w wierzchołkach?
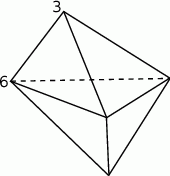
A) 9 B) 12 C) 17 D) 18 E) 24
Ile jest liczb naturalnych  , dla których największy spośród jej dzielników naturalnych różnych od 1 i
, dla których największy spośród jej dzielników naturalnych różnych od 1 i  jest 45 razy większy od najmniejszego spośród tych dzielników?
jest 45 razy większy od najmniejszego spośród tych dzielników?
A) 0 B) 1 C) 2 D) 3 E) Więcej niż 3.
Uzupełniamy tablicę wpisując w każde pole liczbę 0 albo 1, w taki sposób, aby sumy liczb każdego wiersza i każdej kolumny były równe 2. Jakie są wartości  i
i 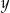 ?
?
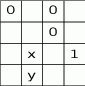
A) 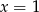 ,
, 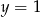 B)
B) 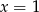 ,
, 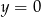 C)
C) 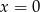 ,
, 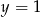 D)
D) 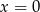 ,
, 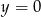 E) Nie można tego ustalić
E) Nie można tego ustalić
Ile liczb trzycyfrowych podzielnych przez 9 ma następującą własność: suma cyfr ilorazu tej liczby przez 9 jest o 9 mniejsza od sumy jej cyfr?
A) 1 B) 2 C) 4 D) 5 E) 11

