Zadanie nr 1763945
Ile jest liczb dziesięciocyfrowych, które można napisać przy użyciu cyfr 1,2 i 3 tak, aby każde dwie sąsiednie cyfry w ich zapisach różniły się o jeden?
A) 16 B) 32 C) 64 D) 80 E) 100
Rozwiązanie
Zacznijmy pisać taką liczbę. Jeżeli na pierwszym miejscu napiszemy 1 lub 3, to na drugim miejscu musi być 2. Wtedy na trzecim miejscu znowu musi być 1 lub 3, na czwartym 2 itd. Mamy zatem 5 miejsc na których muszą być dwójki i 5 miejsc gdzie mogą być 1 lub 3 (dowolnie). Jest więc
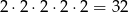
takich liczb. Dokładnie tak samo jest gdy na pierwszym miejscu jest 2, więc w sumie mamy
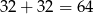
takie liczby.
Odpowiedź: C

