Zadanie nr 4233638
Z jabłek, śliwek, pomarańczy i bananów układamy na półce kompozycje, kładąc kolejno owoc za owocem. Kompozycja jest kompletna, gdy bezpośrednio za owocem dowolnego rodzaju przynajmniej raz leży owoc każdego innego rodzaju. Z ilu owoców składa się najmniej liczna kompletna kompozycja owoców?
A) 13 B) 8 C) 16 D) 4 E) 12
Rozwiązanie
Mamy cztery rodzaje owoców, więc w kompozycji musi się pojawić 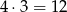 wszystkich możliwych kolejnych par owoców (np. banan, jabłko itp.). Z drugiej strony, jeżeli w kompozycji mamy
wszystkich możliwych kolejnych par owoców (np. banan, jabłko itp.). Z drugiej strony, jeżeli w kompozycji mamy  owoców, to jest w niej
owoców, to jest w niej 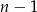 takich par (każdy owoc, z wyjątkiem ostatniego, wyznacza taką parę). Zatem minimalna liczba owoców musi spełniać
takich par (każdy owoc, z wyjątkiem ostatniego, wyznacza taką parę). Zatem minimalna liczba owoców musi spełniać
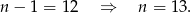
Pozostało napisać taką minimalną kompozycję (żeby sprawdzić, że rzeczywiście 13 jest minimalne).
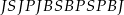
(wypisujemy najpierw pary z jabłkiem na początku, potem z z bananem itd).
Odpowiedź: A

