Zadanie nr 9561260
Powierzchnia bryły narysowanej obok składa się z 6 ścian trójkątnych. W każdym wierzchołku bryły umieszczono liczbę tak, by sumy liczb umieszczonych w wierzchołkach danej ściany były jednakowe dla wszystkich ścian. Dwie liczby 3 i 6 są zaznaczone na rysunku. Ile wynosi suma wszystkich liczb umieszczonych w wierzchołkach?
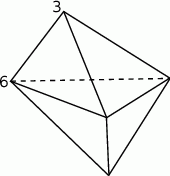
A) 9 B) 12 C) 17 D) 18 E) 24
Rozwiązanie
Zauważmy, że są dwie ściany, które mają krawędź z zaznaczonymi wierzchołkami 3 i 6.
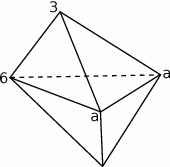
Zatem liczby w trzecich wierzchołkach tych ścian muszą być równe, oznaczmy tę wspólną wartość przez 
. Teraz wystarczy popatrzeć na trójkąt o wierzchołkach z liczbami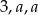 
. Suma liczb w jego wierzchołkach musi być taka sama jak w poprzednich ścianach, więc
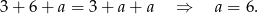
W takim razie w dolnym wierzchołku musi być wpisane 3. Suma wszystkich liczb to
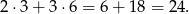
Odpowiedź: E
