Zadanie nr 9613577
Ile jest liczb naturalnych  , dla których największy spośród jej dzielników naturalnych różnych od 1 i
, dla których największy spośród jej dzielników naturalnych różnych od 1 i  jest 45 razy większy od najmniejszego spośród tych dzielników?
jest 45 razy większy od najmniejszego spośród tych dzielników?
A) 0 B) 1 C) 2 D) 3 E) Więcej niż 3.
Rozwiązanie
Jeżeli  jest najmniejszym dzielnikiem liczby
jest najmniejszym dzielnikiem liczby  , to największym dzielnikiem jest
, to największym dzielnikiem jest 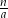 . Mamy więc równanie
. Mamy więc równanie
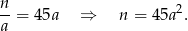
W szczególności  musi dzielić się przez 45, więc też przez 3. To jednak oznacza, że
musi dzielić się przez 45, więc też przez 3. To jednak oznacza, że 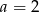 lub
lub 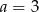 (bo
(bo  miało być najmniejszym dzielnikiem). Daje to nam dwie liczby:
miało być najmniejszym dzielnikiem). Daje to nam dwie liczby:
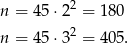
Odpowiedź: C

