Zadania.info
Największy internetowy zbiór zadań z matematyki
cornersUpL
cornersUpR

Zadania

Na skróty

Recenzje

Linki sponsorowane

cornersM
Zaloguj się

Linki sponsorowane

cornersR
Zadanie nr 6318013

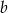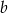Na różnych prostych równoległych a i b obrano 6 punktów: 4 punkty na prostej a i 2 punkty na prostej b . Ile jest trójkątów, których wszystkie wierzchołki są w wybranych punktach?
A) 6 B) 8 C) 12 D) 16 E) 18

Wersja PDF
Rozwiązanie

Zróbmy pomocniczy rysunek.

PIC

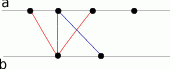
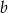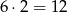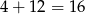Są dwa rodzaje trójkątów – te które mają podstawę na prostej a i te z podstawą na prostej b . Tych drugich jest 4. Tych pierwszych jest tyle ile wyborów dwóch punktów spośród 4, czyli 6, pomnożone przez możliwe wybory trzeciego wierzchołka, czyli razem 6 ⋅2 = 12 . Wszystkich trójkątów jest 4 + 12 = 16 .  
Odpowiedź: D

Wersja PDF
Twoje uwagi
Nie rozumiesz fragmentu rozwiązania?
W rozwiązaniu jest błąd lub literówka?
Masz inny pomysł na rozwiązanie tego zadania?
Napisz nam o tym!