Wierzchołkami kwadratu 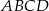 są punkty o współrzędnych
są punkty o współrzędnych 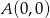 ,
, 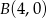 ,
, 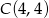 i
i 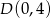 . Dla każdej liczby rzczywistej
. Dla każdej liczby rzczywistej 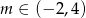 rozważamy trójkąt o wierzchołkach
rozważamy trójkąt o wierzchołkach 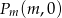 ,
, 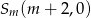 i
i 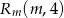 . Wyznacz wszystkie wartości prametru
. Wyznacz wszystkie wartości prametru 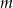 , dla których pole figury, która jest częścią wspólną kwadratu
, dla których pole figury, która jest częścią wspólną kwadratu 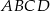 i trójkąta
i trójkąta 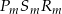 wynosi 2.
wynosi 2.
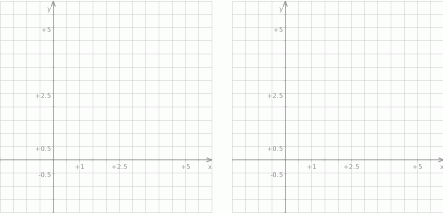

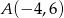 , która wraz z osiami układu współrzędnych ogranicza trójkąt o polu równym 2.
, która wraz z osiami układu współrzędnych ogranicza trójkąt o polu równym 2. 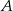 i
i 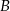 kwadratu
kwadratu 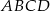 leżą na paraboli
leżą na paraboli 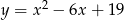 , przy czym odcinek
, przy czym odcinek 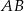 jest równoległy do osi
jest równoległy do osi 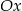 . Wykaż, że jeżeli odległość punktu
. Wykaż, że jeżeli odległość punktu 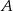 od osi
od osi 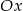 jest liczbą całkowitą to pole kwadratu
jest liczbą całkowitą to pole kwadratu 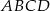 również jest liczbą całkowitą.
również jest liczbą całkowitą. 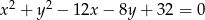 wpisano trójkąt równoboczny
wpisano trójkąt równoboczny 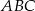 w którym
w którym 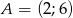 . Oblicz współrzędne pozostałych wierzchołków trójkąta.
. Oblicz współrzędne pozostałych wierzchołków trójkąta. 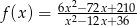 określonej dla
określonej dla 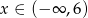 . Wykres ten przecina osie
. Wykres ten przecina osie 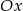 i
i 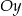 odpowiednio w punktach
odpowiednio w punktach 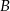 i
i 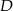 , a punkt
, a punkt 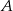 jest początkiem układu współrzędnych. Rozpatrujemy wszystkie czworokąty
jest początkiem układu współrzędnych. Rozpatrujemy wszystkie czworokąty 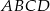 , w których punkt
, w których punkt 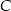 leży na wykresie funkcji
leży na wykresie funkcji 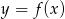 pomiędzy punktami
pomiędzy punktami 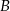 i
i 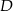 .
. 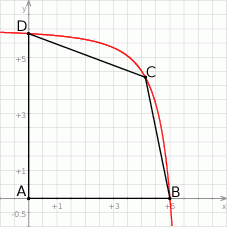
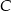 tego z rozpatrywanych czworokątów, którego pole jest największe.
tego z rozpatrywanych czworokątów, którego pole jest największe. 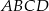 :
: 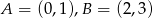 . Wyznacz współrzędne wierzchołka
. Wyznacz współrzędne wierzchołka 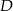 , jeśli wiesz, że kwadrat jest zawarty w I i II ćwiartce układu współrzędnych.
, jeśli wiesz, że kwadrat jest zawarty w I i II ćwiartce układu współrzędnych. 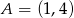 i
i 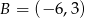 leży na osi
leży na osi 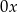 .
. 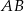 i oddalonej od początku układu współrzędnych o
i oddalonej od początku układu współrzędnych o 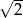 .
.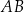 trójkąta
trójkąta 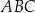 o wierzchołkach
o wierzchołkach 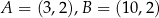 i
i 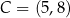 .
. 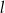 , na której leży punkt
, na której leży punkt 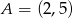 , przecina parabolę o równaniu
, przecina parabolę o równaniu 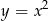 w dwóch różnych punktach
w dwóch różnych punktach 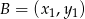 i
i 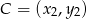 . Oblicz wartość współczynnika kierunkowego prostej
. Oblicz wartość współczynnika kierunkowego prostej 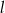 , przy której suma
, przy której suma 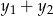 osiągnie wartość najmniejszą.
osiągnie wartość najmniejszą. 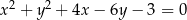 i zarazem prostopadłych do prostej
i zarazem prostopadłych do prostej 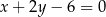 .
. 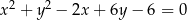 i zarazem prostopadłych do prostej
i zarazem prostopadłych do prostej 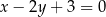 .
. 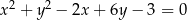 i zarazem prostopadłych do prostej
i zarazem prostopadłych do prostej 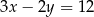 .
. 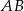 i
i 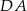 rombu
rombu 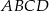 są zawarte odpowiednio w prostych o równaniach
są zawarte odpowiednio w prostych o równaniach 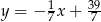 i
i 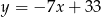 . Napisz równanie prostej zawierającej przekątną
. Napisz równanie prostej zawierającej przekątną 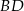 tego rombu, jeżeli jego środek ma współrzędne
tego rombu, jeżeli jego środek ma współrzędne 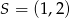 .
. 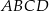 , w którym
, w którym 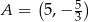 . Przekątna
. Przekątna 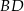 tego kwadratu jest zawarta w prostej o równaniu
tego kwadratu jest zawarta w prostej o równaniu 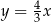 . Oblicz współrzędne punktu przecięcia przekątnych
. Oblicz współrzędne punktu przecięcia przekątnych 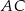 i
i 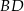 oraz pole kwadratu
oraz pole kwadratu 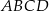 .
. 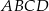 , w którym
, w którym 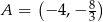 . Przekątna
. Przekątna 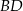 tego kwadratu jest zawarta w prostej o równaniu
tego kwadratu jest zawarta w prostej o równaniu 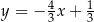 . Oblicz współrzędne punktu przecięcia przekątnych
. Oblicz współrzędne punktu przecięcia przekątnych 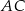 i
i 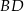 oraz pole kwadratu
oraz pole kwadratu 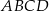 .
. 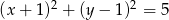 poprowadzonych z punktu
poprowadzonych z punktu 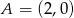 .
. 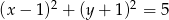 poprowadzonych z punktu
poprowadzonych z punktu 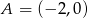 .
. 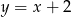 oraz
oraz 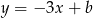 , które przecinają się w punkcie leżącym na osi
, które przecinają się w punkcie leżącym na osi 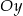 układu współrzędnych. Oblicz pole trójkąta, którego dwa boki zawierają się w danych prostych, a trzeci jest zawarty w osi
układu współrzędnych. Oblicz pole trójkąta, którego dwa boki zawierają się w danych prostych, a trzeci jest zawarty w osi 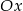 .
. 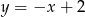 oraz
oraz 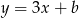 , które przecinają się w punkcie leżącym na osi
, które przecinają się w punkcie leżącym na osi 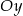 układu współrzędnych. Oblicz pole trójkąta, którego dwa boki zawierają się w danych prostych, a trzeci jest zawarty w osi
układu współrzędnych. Oblicz pole trójkąta, którego dwa boki zawierają się w danych prostych, a trzeci jest zawarty w osi 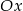 .
. 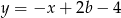 oraz
oraz 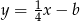 , które przecinają się w punkcie leżącym na osi
, które przecinają się w punkcie leżącym na osi 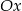 układu współrzędnych. Oblicz pole trójkąta, którego dwa boki zawierają się w danych prostych, a trzeci jest zawarty w osi
układu współrzędnych. Oblicz pole trójkąta, którego dwa boki zawierają się w danych prostych, a trzeci jest zawarty w osi 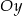 .
. 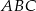 , którego boki zawierają się w prostych o równaniach:
, którego boki zawierają się w prostych o równaniach: 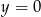 ,
, 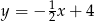 oraz
oraz 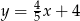 .
. 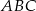 , którego boki zawierają się w prostych o równaniach:
, którego boki zawierają się w prostych o równaniach: 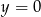 ,
, 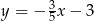 oraz
oraz 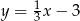 .
. 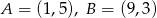 i prosta
i prosta 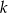 o równaniu
o równaniu 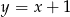 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 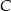 leżącego na prostej
leżącego na prostej 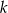 , dla którego suma
, dla którego suma 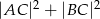 jest najmniejsza.
jest najmniejsza. 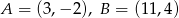 . Na prostej o równaniu
. Na prostej o równaniu 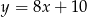 znajdź punkt
znajdź punkt 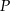 , dla którego suma
, dla którego suma 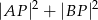 jest najmniejsza.
jest najmniejsza. 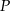 leżącego na prostej o równaniu
leżącego na prostej o równaniu 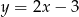 , którego suma kwadratów odległości od punktów
, którego suma kwadratów odległości od punktów 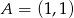 i
i 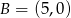 jest najmniejsza.
jest najmniejsza. 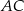 rombu
rombu 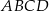 jest zawarta w prostej o równaniu
jest zawarta w prostej o równaniu 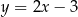 . Wierzchołki
. Wierzchołki 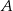 i
i 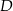 mają współrzędne
mają współrzędne 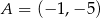 i
i 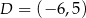 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków 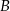 i
i 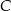 oraz pole rombu
oraz pole rombu 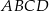 .
. 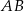 trójkąta równoramiennego
trójkąta równoramiennego 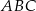 jest zawarta w prostej o równaniu
jest zawarta w prostej o równaniu 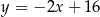 . Wierzchołki
. Wierzchołki 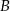 i
i 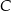 mają współrzędne
mają współrzędne 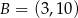 i
i 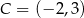 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 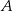 i pole trójkąta
i pole trójkąta 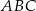 .
. 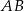 trójkąta równoramiennego
trójkąta równoramiennego 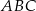 jest zawarta w prostej o równaniu
jest zawarta w prostej o równaniu 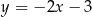 . Wierzchołki
. Wierzchołki 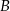 i
i 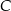 mają współrzędne
mają współrzędne 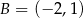 i
i 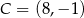 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 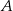 i pole trójkąta
i pole trójkąta 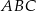 .
. 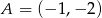 oraz
oraz 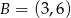 . Odcinek
. Odcinek 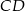 jest obrazem odcinka
jest obrazem odcinka 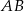 zarówno w jednokładności o dodatniej skali i środku
zarówno w jednokładności o dodatniej skali i środku 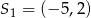 , jak i w jednokładności o ujemnej skali i środku
, jak i w jednokładności o ujemnej skali i środku 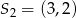 . Oblicz współrzędne końców odcinka
. Oblicz współrzędne końców odcinka 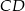 oraz skalę jednokładności o środku
oraz skalę jednokładności o środku 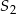 .
. 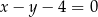 znajdź punkt
znajdź punkt 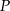 , którego kwadrat odległości od punktu
, którego kwadrat odległości od punktu 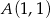 jest najmniejszy.
jest najmniejszy. 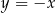 wyznacz współrzędne punktu
wyznacz współrzędne punktu 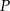 leżącego najbliżej punktu
leżącego najbliżej punktu 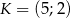 .
. 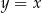 wyznacz współrzędne punktu
wyznacz współrzędne punktu 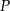 leżącego najbliżej punktu
leżącego najbliżej punktu 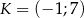 .
. 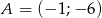 ,
, 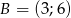 ,
, 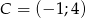 są wierzchołkami trapezu. Ramię trapezu
są wierzchołkami trapezu. Ramię trapezu 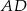 jest prostopadłe do podstaw
jest prostopadłe do podstaw 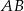 i
i 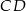 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 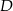 oraz pole powierzchni tego trapezu.
oraz pole powierzchni tego trapezu. 