Dany jest romb o środku symetrii 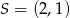 . Bok
. Bok 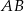 jest równoległy do prostej o równaniu
jest równoległy do prostej o równaniu 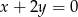 . Wektor
. Wektor 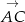 ma współrzędne
ma współrzędne ![[12 ,6 ]](https://img.zadania.info/zad/9275549/HzadT4x.gif) .
.
- Wyznacz współrzędne wszystkich wierzchołków rombu.
- Sprawdź czy miara kąta
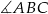 jest większa niż
jest większa niż 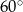 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dany jest romb o środku symetrii 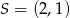 . Bok
. Bok 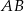 jest równoległy do prostej o równaniu
jest równoległy do prostej o równaniu 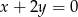 . Wektor
. Wektor 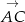 ma współrzędne
ma współrzędne ![[12 ,6 ]](https://img.zadania.info/zad/9275549/HzadT4x.gif) .
.
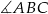 jest większa niż
jest większa niż 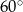 .
.Wierzchołki 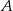 i
i 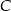 kwadratu
kwadratu 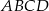 o polu 8 leżą na prostej o równaniu
o polu 8 leżą na prostej o równaniu 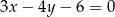 . Środek symetrii tego kwadratu ma współrzędne
. Środek symetrii tego kwadratu ma współrzędne 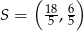 . Oblicz współrzędne punktów
. Oblicz współrzędne punktów 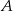 i
i 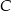 .
.
Wyznacz współrzędne punktu 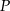 , który dzieli odcinek o końcach
, który dzieli odcinek o końcach 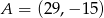 i
i 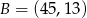 w stosunku
w stosunku 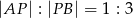 .
.
Wyznacz współrzędne punktu 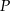 , który dzieli odcinek o końcach
, który dzieli odcinek o końcach 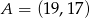 i
i 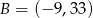 w stosunku
w stosunku 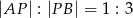 .
.
Punkt 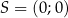 jest środkiem boku
jest środkiem boku 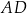 równoległoboku
równoległoboku 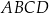 . Wiadomo też, że
. Wiadomo też, że ![−→ AB = [4;3]](https://img.zadania.info/zad/9290117/HzadT3x.png) oraz
oraz ![−→ BC = [6;2]](https://img.zadania.info/zad/9290117/HzadT4x.png) . Wyznacz wierzchołki tego równoległoboku.
. Wyznacz wierzchołki tego równoległoboku.
Wykaż, że prosta 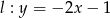 jest styczna do okręgu
jest styczna do okręgu 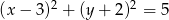 .
.
Sprawdź, czy prosta 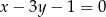 jest styczna do okręgu
jest styczna do okręgu 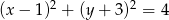 .
.
Punkt 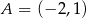 jest wierzchołkiem rombu o polu równym 20. Punkt
jest wierzchołkiem rombu o polu równym 20. Punkt 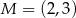 jest środkiem symetrii tego rombu. Wyznacz równanie okręgu wpisanego w ten romb.
jest środkiem symetrii tego rombu. Wyznacz równanie okręgu wpisanego w ten romb.
Dane są punkty 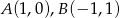 . Punkt
. Punkt 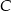 należy do okręgu o równaniu
należy do okręgu o równaniu 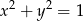 . Znajdź współrzędne punktu
. Znajdź współrzędne punktu 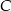 tak, aby pole trójkąta
tak, aby pole trójkąta  było największe. Oblicz to pole.
było największe. Oblicz to pole.
Dane są punkty 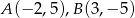 . Punkt
. Punkt 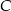 należy do okręgu o równaniu
należy do okręgu o równaniu 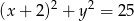 . Znajdź współrzędne punktu
. Znajdź współrzędne punktu 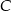 tak, aby pole trójkąta
tak, aby pole trójkąta 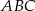 było największe. Oblicz to pole.
było największe. Oblicz to pole.
Wyznacz równanie prostych przechodzących przez początek układu współrzędnych i stycznych do okręgu o środku w punkcie 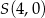 i promieniu
i promieniu 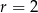 .
.
Znajdź równanie krzywej, którą tworzą wszystkie punkty jednakowo odległe od okręgu 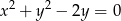 i od prostej
i od prostej 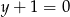 .
.
Wyznacz współrzędne punktu przecięcia się przekątnych czworokąta 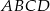 jeżeli
jeżeli 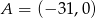 ,
, 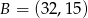 ,
, 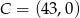 i
i 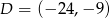 .
.
Punkt 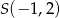 jest środkiem okręgu opisanego na trójkącie
jest środkiem okręgu opisanego na trójkącie 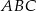 . Wierzchołek
. Wierzchołek 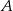 ma współrzędne
ma współrzędne 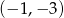 , a bok
, a bok 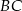 jest zawarty w prostej o równaniu
jest zawarty w prostej o równaniu 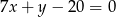 . Oblicz pole trójkąta
. Oblicz pole trójkąta 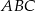 .
.
W układzie współrzędnych punkty 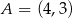 i
i 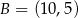 są wierzchołkami trójkąta
są wierzchołkami trójkąta 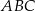 . Wierzchołek
. Wierzchołek 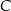 leży na prostej o równaniu
leży na prostej o równaniu 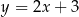 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 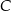 , dla którego kąt
, dla którego kąt 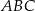 jest prosty.
jest prosty.
W układzie współrzędnych punkty 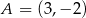 i
i 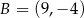 są wierzchołkami trójkąta
są wierzchołkami trójkąta 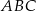 . Wierzchołek
. Wierzchołek 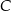 leży na prostej o równaniu
leży na prostej o równaniu 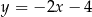 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 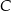 , dla którego kąt
, dla którego kąt 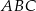 jest prosty.
jest prosty.
Wyznacz równanie symetralnej odcinka o końcach 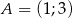 i
i 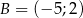 .
.
Wyznacz równanie symetralnej odcinka 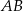 , gdzie
, gdzie 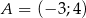 i
i 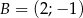 .
.
Wyznacz równanie symetralnej odcinka o końcach 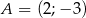 i
i 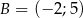 .
.
Wyznacz równanie symetralnej odcinka o końcach 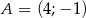 i
i 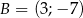 .
.
Wyznacz równanie symetralnej odcinka o końcach 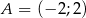 i
i 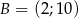 .
.
Dany jest odcinek o końcach 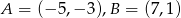 .
.
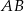 .
.Dany jest odcinek o końcach 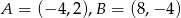 .
.
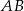 .
. 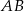 .
.Wyznacz równanie prostej przechodzącej przez początek układu współrzędnych i przez środek okręgu o równaniu 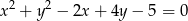 .
.
Wyznacz równanie prostej przechodzącej przez początek układu współrzędnych i przez środek okręgu o równaniu 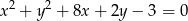 .
.
Wyznacz równanie prostej przechodzącej przez początek układu współrzędnych i przez środek okręgu o równaniu 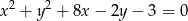 .
.
Punkty 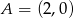 i
i 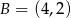 leżą na okręgu o równaniu
leżą na okręgu o równaniu 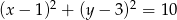 . Wyznacz na tym okręgu taki punkt
. Wyznacz na tym okręgu taki punkt 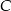 , aby trójkąt
, aby trójkąt 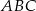 był trójkątem równoramiennym o podstawie
był trójkątem równoramiennym o podstawie 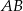 .
.
Punkty 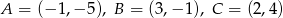 są kolejnymi wierzchołkami równoległoboku
są kolejnymi wierzchołkami równoległoboku 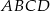 . Oblicz pole tego równoległoboku.
. Oblicz pole tego równoległoboku.
Oblicz pole równoległoboku 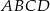 o wierzchołkach
o wierzchołkach 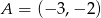 ,
, 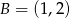 ,
, 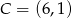 ,
, 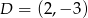 .
.
Dane są punkty 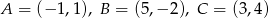 .
.
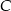 i prostopadłej do prostej
i prostopadłej do prostej 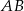 .
.  .
.Ile punktów wspólnych ma prosta 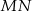 z okręgiem
z okręgiem 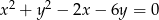 jeśli
jeśli 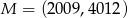 oraz
oraz 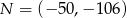 .
.
W równoległoboku 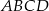 dane są wierzchołki
dane są wierzchołki 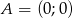 ,
, 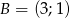 ,
, 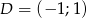 . Wyznacz wierzchołek
. Wyznacz wierzchołek 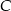 oraz środek symetrii tego równoległoboku.
oraz środek symetrii tego równoległoboku.
Wyznacz współrzędne wierzchołka 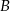 równoległoboku
równoległoboku 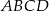 jeżeli
jeżeli 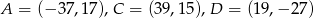 .
.
