W układzie współrzędnych na płaszczyźnie punkty 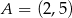 i
i 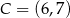 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 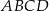 . Wyznacz równanie prostej
. Wyznacz równanie prostej 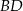 .
.
/Szkoła średnia/Geometria/Geometria analityczna
W kwadracie 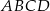 punkty
punkty 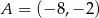 oraz
oraz 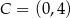 są końcami przekątnej. Wyznacz równanie prostej zawierającej przekątną
są końcami przekątnej. Wyznacz równanie prostej zawierającej przekątną 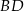 tego kwadratu.
tego kwadratu.
W układzie współrzędnych na płaszczyźnie punkty 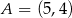 i
i 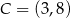 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 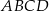 . Wyznacz równanie prostej
. Wyznacz równanie prostej 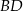 .
.
Wierzchołek 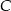 trójkąta
trójkąta 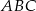 leży na prostej
leży na prostej 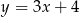 , a pozostałe wierzchołki mają współrzędne
, a pozostałe wierzchołki mają współrzędne 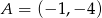 i
i 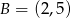 . Uzasadnij, że pole trójkąta
. Uzasadnij, że pole trójkąta 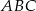 nie zależy od wyboru punktu
nie zależy od wyboru punktu 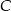 i oblicz to pole.
i oblicz to pole.
Pole równoległoboku 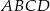 o danych wierzchołkach
o danych wierzchołkach 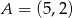 i
i 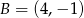 jest równe 26. Wyznacz współrzędne pozostałych wierzchołków równoległoboku, jeżeli jego przekątne przecinają się w punkcie leżącym na prostej
jest równe 26. Wyznacz współrzędne pozostałych wierzchołków równoległoboku, jeżeli jego przekątne przecinają się w punkcie leżącym na prostej 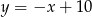 , który ma obie współrzędne będące liczbami całkowitymi.
, który ma obie współrzędne będące liczbami całkowitymi.
Dane są wektory: ![→ u = [2;− 4]](https://img.zadania.info/zad/9899559/HzadT0x.gif) ,
, ![→ v = [− 3;5]](https://img.zadania.info/zad/9899559/HzadT1x.gif) . Oblicz
. Oblicz 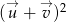 .
.
Dane są wektory: ![→ u = [2;− 4]](https://img.zadania.info/zad/2354795/HzadT0x.gif) ,
, ![→ v = [− 3;5]](https://img.zadania.info/zad/2354795/HzadT1x.gif) . Oblicz
. Oblicz 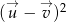 .
.
Dane są wektory: ![→ u = [2;− 4]](https://img.zadania.info/zad/7943696/HzadT0x.gif) ,
, ![→ v = [− 3;5]](https://img.zadania.info/zad/7943696/HzadT1x.gif) . Oblicz
. Oblicz 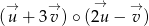 .
.
W układzie współrzędnych dane są dwa punkty: 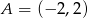 i
i 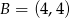 .
.
- Wyznacz równanie symetralnej odcinka
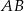 .
. - Prosta
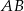 oraz prosta o równaniu
oraz prosta o równaniu 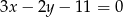 przecinają się w punkcie
przecinają się w punkcie 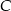 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 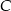 .
.
Wyznacz współrzędne środka jednokładności, w której obrazem okręgu o równaniu 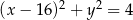 jest okrąg o równaniu
jest okrąg o równaniu 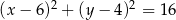 , a skala tej jednokładności jest liczbą ujemną.
, a skala tej jednokładności jest liczbą ujemną.
Ostrokątny trójkąt równoramienny 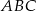 o podstawie
o podstawie 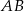 jest wpisany w okrąg o równaniu
jest wpisany w okrąg o równaniu 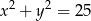 . Punkty
. Punkty 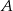 i
i 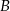 leżą na prostej o równaniu
leżą na prostej o równaniu 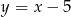 .
.
- Oblicz współrzędne punktów:
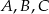 .
. - Oblicz kąty trójkąta
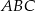 .
.
Prosta 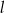 przecina okrąg o środku
przecina okrąg o środku 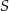 w punktach
w punktach 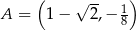 i
i 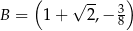 . Punkt
. Punkt  leży na prostej
leży na prostej 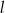 . Oblicz pole koła ograniczonego tym okręgiem.
. Oblicz pole koła ograniczonego tym okręgiem.
Przekształcenie 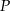 określone jest w następujący sposób:
określone jest w następujący sposób: 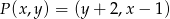 , gdzie
, gdzie 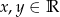 .
.
- Wykaż, że przekształcenie
 jest izometrią.
jest izometrią. - W prostokątnym układzie współrzędnych narysuj trójkąt o wierzchołkach
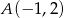 ,
, 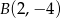 ,
, 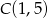 , a następnie znajdź jego obraz w przekształceniu
, a następnie znajdź jego obraz w przekształceniu 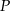 .
. - Wyznacz równanie prostej zawierającej wysokość trójkąta
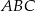 poprowadzoną na bok
poprowadzoną na bok 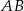 .
. - Oblicz pole trójkąta
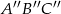 , który jest obrazem trójkąta
, który jest obrazem trójkąta 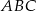 w jednokładności o środku w punkcie (0,0) i skali
w jednokładności o środku w punkcie (0,0) i skali 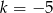 .
.
Wyznacz równanie okręgu o środku 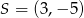 przechodzącego przez początek układu współrzędnych.
przechodzącego przez początek układu współrzędnych.
Wyznacz równanie okręgu o środku 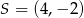 przechodzącego przez punkt
przechodzącego przez punkt 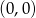 .
.
W kartezjańskim układzie współrzędnych 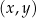 środek
środek 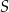 okręgu o promieniu
okręgu o promieniu 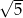 leży na prostej o równaniu
leży na prostej o równaniu 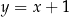 . Przez punkt
. Przez punkt 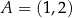 , którego odległość od punktu
, którego odległość od punktu 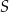 jest większa od
jest większa od 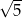 , poprowadzono dwie proste styczne do tego okręgu w punktach – odpowiednio –
, poprowadzono dwie proste styczne do tego okręgu w punktach – odpowiednio – 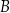 i
i 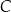 . Pole czworokąta
. Pole czworokąta 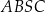 jest równe 15. Oblicz współrzędne punktu
jest równe 15. Oblicz współrzędne punktu 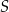 . Rozważ wszystkie przypadki.
. Rozważ wszystkie przypadki.

