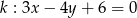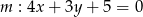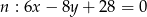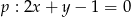Dane są dwa przeciwległe wierzchołki 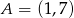 i
i 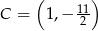 prostokąta
prostokąta 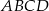 . Prosta o równaniu
. Prosta o równaniu 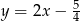 jest osią symetrii tego prostokąta. Oblicz współrzędne wierzchołków
jest osią symetrii tego prostokąta. Oblicz współrzędne wierzchołków 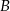 i
i 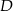 tego prostokąta.
tego prostokąta.
/Szkoła średnia/Geometria/Geometria analityczna
Boki 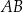 i
i 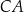 trójkąta
trójkąta 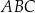 są zawarte w prostych
są zawarte w prostych 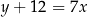 i
i 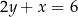 , a jego dwa wierzchołki mają współrzędne
, a jego dwa wierzchołki mają współrzędne 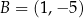 i
i 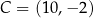 . Oblicz pole tego trójkąta.
. Oblicz pole tego trójkąta.
W trójkącie 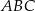 o polu 20 dane sa współrzędne dwóch wierzchołków:
o polu 20 dane sa współrzędne dwóch wierzchołków:  ,
, 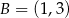 oraz środek
oraz środek 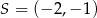 okręgu opisanego na tym trójkącie. Wyznacz współrzędne wierzchołka
okręgu opisanego na tym trójkącie. Wyznacz współrzędne wierzchołka 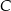 .
.
Figura 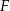 jest sumą dwóch prostych o równaniach
jest sumą dwóch prostych o równaniach 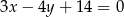 oraz
oraz 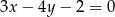 . Sprawdź czy podana prosta jest osią symetrii tej figury:
. Sprawdź czy podana prosta jest osią symetrii tej figury:
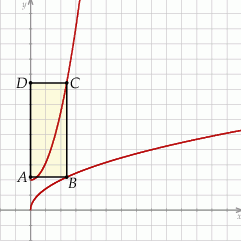
Rozpatrujemy prostokąty 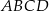 , których dwa wierzchołki leżą na osi
, których dwa wierzchołki leżą na osi 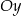 , jeden wierzchołek leży na paraboli określonej równaniem
, jeden wierzchołek leży na paraboli określonej równaniem 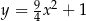 , jeden wierzchołek leży na wykresie funkcji
, jeden wierzchołek leży na wykresie funkcji 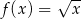 określonej dla
określonej dla 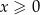 . Oblicz pole tego z tych prostokątów, który ma najmniejszy możliwy obwód.
. Oblicz pole tego z tych prostokątów, który ma najmniejszy możliwy obwód.
Wierzchołki trapezu 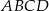 mają współrzędne:
mają współrzędne: 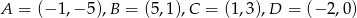 . Napisz równanie okręgu, który jest styczny do podstawy
. Napisz równanie okręgu, który jest styczny do podstawy 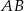 tego trapezu, a jego środek jest punktem przecięcia się prostych zawierających ramiona
tego trapezu, a jego środek jest punktem przecięcia się prostych zawierających ramiona 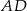 oraz
oraz 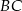 trapezu
trapezu 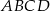 .
.
Wierzchołki trapezu 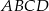 mają współrzędne:
mają współrzędne: 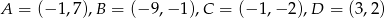 . Napisz równanie okręgu, który jest styczny do podstawy
. Napisz równanie okręgu, który jest styczny do podstawy 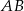 tego trapezu, a jego środek jest punktem przecięcia się przekątnych trapezu
tego trapezu, a jego środek jest punktem przecięcia się przekątnych trapezu 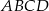 .
.
Napisz równanie okręgu o środku 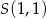 , który na prostej o równaniu
, który na prostej o równaniu 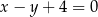 odcina cięciwę
odcina cięciwę 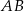 długości
długości 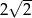 . Wykonaj rysunek.
. Wykonaj rysunek.
Prosta o równaniu 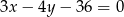 przecina okrąg o środku
przecina okrąg o środku 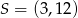 w punktach
w punktach 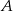 i
i 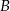 . Długość odcinka
. Długość odcinka 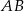 jest równa 40. Wyznacz równanie tego okręgu.
jest równa 40. Wyznacz równanie tego okręgu.
Dane są punkty 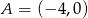 i
i 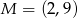 oraz prosta
oraz prosta 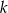 o równaniu
o równaniu 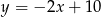 . Wierzchołek
. Wierzchołek 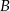 trójkąta
trójkąta 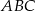 to punkt przecięcia prostej
to punkt przecięcia prostej 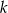 z osią
z osią 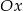 układu współrzędnych, a wierzchołek
układu współrzędnych, a wierzchołek 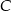 jest punktem przecięcia prostej
jest punktem przecięcia prostej 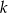 z prostą
z prostą 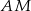 . Oblicz pole trójkąta
. Oblicz pole trójkąta 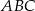 .
.
Dane są punkty 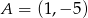 i
i 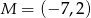 oraz prosta
oraz prosta 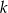 o równaniu
o równaniu 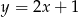 . Wierzchołek
. Wierzchołek 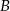 trójkąta
trójkąta 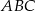 to punkt przecięcia prostej
to punkt przecięcia prostej 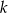 z prostą
z prostą 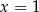 , a wierzchołek
, a wierzchołek 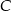 jest punktem przecięcia prostej
jest punktem przecięcia prostej 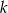 z prostą
z prostą 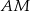 . Oblicz pole trójkąta
. Oblicz pole trójkąta 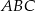 .
.
Rozpatrujemy wszystkie prostokąty o polu równym 6, których dwa sąsiednie boki zawarte są w osiach 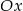 i
i 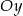 układu współrzędnych. Wyznacz równanie krzywej będącej zbiorem tych wierzchołków rozpatrywanych prostokątów, które nie leżą na żadnej z osi układu współrzędnych. Narysuj tę krzywą.
układu współrzędnych. Wyznacz równanie krzywej będącej zbiorem tych wierzchołków rozpatrywanych prostokątów, które nie leżą na żadnej z osi układu współrzędnych. Narysuj tę krzywą.
Wyznacz figurę, która jest zbiorem środków cięciw paraboli 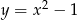 przechodzących przez początek układu współrzędnych.
przechodzących przez początek układu współrzędnych.
Dany jest równoległobok 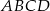 o wierzchołkach
o wierzchołkach 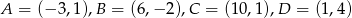 . Napisz równania prostych, w których zawarte są przekątne równoległoboku.
. Napisz równania prostych, w których zawarte są przekątne równoległoboku.
Dany jest wierzchołek trójkąta równobocznego 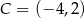 . Bok
. Bok 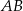 zawarty jest w prostej o równaniu
zawarty jest w prostej o równaniu 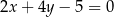 . Wyznacz długość boku tego trójkąta.
. Wyznacz długość boku tego trójkąta.
Punkty 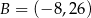 ,
, 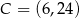 i
i 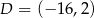 są wierzchołkami trapezu równoramiennego
są wierzchołkami trapezu równoramiennego 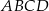 o podstawach
o podstawach 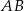 i
i 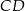 . Wyznacz współrzędne wierzchołka
. Wyznacz współrzędne wierzchołka 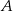 tego trapezu jeżeli wiadomo, że
tego trapezu jeżeli wiadomo, że 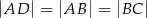 .
.
Punkty 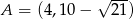 i
i 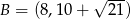 są wierzchołkami trójkąta prostokątnego
są wierzchołkami trójkąta prostokątnego 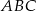 , o kącie prostym przy wierzchołku
, o kącie prostym przy wierzchołku 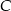 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 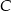 tego trójkąta, wiedząc, że leży on na paraboli o równaniu
tego trójkąta, wiedząc, że leży on na paraboli o równaniu 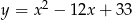 .
.
Wyznacz środek okręgu przechodzącego przez punkty 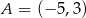 i
i 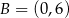 , którego środek leży na prostej o równaniu
, którego środek leży na prostej o równaniu 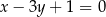 .
.
Dany jest równoległobok, którego boki zawierają się w prostych o równaniach: 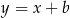 ,
, 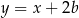 ,
, 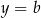 ,
, 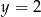 , gdzie liczba rzeczywista
, gdzie liczba rzeczywista 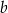 spełnia warunki:
spełnia warunki: 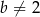 i
i 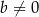 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 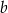 , dla których pole tego równoległoboku jest równe 1.
, dla których pole tego równoległoboku jest równe 1.
Dany jest równoległobok, którego boki zawierają się w prostych o równaniach: 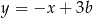 ,
, 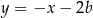 ,
, 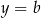 ,
, 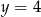 , gdzie liczba rzeczywista
, gdzie liczba rzeczywista 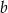 spełnia warunki:
spełnia warunki: 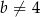 i
i 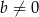 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 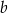 , dla których pole tego równoległoboku jest równe 20.
, dla których pole tego równoległoboku jest równe 20.
Proste o równaniach: 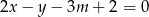 i
i 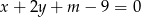 przecinają się w punkcie
przecinają się w punkcie 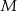 . Dla jakich wartości
. Dla jakich wartości 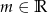 punkt
punkt 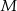 należy do prostej o równaniu
należy do prostej o równaniu 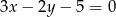 .
.
Wykaż, że jeżeli punkt 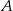 leży na prostej
leży na prostej 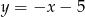 , a punkt
, a punkt 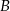 ma współrzędne
ma współrzędne
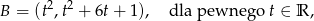
to długość odcinka 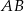 jest nie mniejsza niż
jest nie mniejsza niż 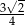 .
.
Punkt 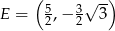 jest środkiem boku
jest środkiem boku 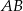 trójkąta równobocznego
trójkąta równobocznego 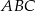 , a boki
, a boki 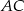 i
i 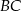 tego trójkąta są zawarte odpowiednio w prostych o równaniach
tego trójkąta są zawarte odpowiednio w prostych o równaniach 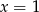 i
i 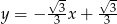 . Wyznacz współrzędne wierzchołków tego trójkąta.
. Wyznacz współrzędne wierzchołków tego trójkąta.
W okrąg o środku 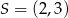 wpisano trapez w taki sposób, że jedna podstawa jest średnicą okręgu, a druga jest zawarta w prostej o równaniu
wpisano trapez w taki sposób, że jedna podstawa jest średnicą okręgu, a druga jest zawarta w prostej o równaniu 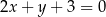 . Pole tego trapezu jest równe
. Pole tego trapezu jest równe 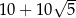 . Oblicz współrzędne tych wierzchołków trapezu, które są końcami jego krótszej podstawy.
. Oblicz współrzędne tych wierzchołków trapezu, które są końcami jego krótszej podstawy.