/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 1153290

Dodaj do ulubionych
Dodaj do rozwiązanych

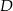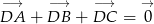Udowodnij, że jeżeli punkt D jest środkiem ciężkości trójkąta, to −→ −→ −→ → DA + DB + DC = 0 .

Rozwiązanie

Sposób I

Rysujemy trójkąt i jego środkowe 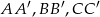AA ′,BB ′,CC ′ .

PIC

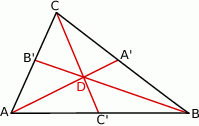
Spróbujemy wyrazić wektory 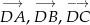−→ −→ − → DA ,DB ,DC w zależności od wektorów 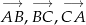− → −→ −→ AB ,BC ,CA wyznaczonych przez boki trójkąta. Korzystamy z faktu, że środkowe dzielą się w stosunku 2:1.

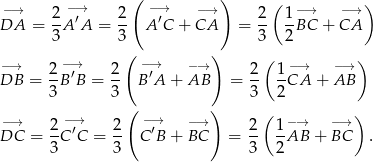
( ) ( ) −→ 2 − →′ 2 −→′ −→ 2 1 −→ −→ DA = --A A = -- A C + CA = -- --BC + CA 3 3( ) 3 2 − → 2 −→ 2 −→ −→ 2 ( 1 −→ −→ ) DB = -B ′B = -- B ′A + AB = -- -CA + AB 3 3 3 2 −→ ( −→ ) ( ) −→ 2- ′ 2- ′ −→ 2- 1-−→ −→ DC = 3 C C = 3 C B + BC = 3 2AB + BC .

W takim razie

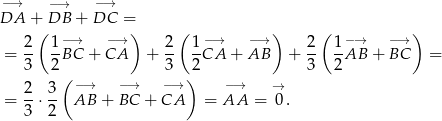
−→ − → −→ DA + DB + DC = ( −→ −→ ) ( −→ −→ ) ( −→ −→ ) = 2- 1BC + CA + 2- 1CA + AB + 2- 1-AB + BC = 3 2 3 2 3 2 2 3 ( −→ −→ −→ ) − → → = --⋅-- AB + BC + CA = AA = 0 . 3 2

Sposób II

Umieśćmy trójkąt 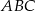ABC w układzie współrzędnych tak, aby 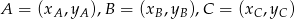A = (xA ,yA ),B = (xB ,yB),C = (xC,yC ) . Jak wiadomo środek ciężkości ma wtedy współrzędne

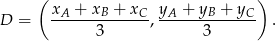
( ) xA-+--xB +-xC- yA-+-yB-+-yC-- D = 3 , 3 .

Mamy zatem

−→ −→ −→ DA + DB + DC = [ ] = xA − xA-+--xB +-xC-,yA − yA-+--yB-+-yC- + 3 3 [ xA + xB + xC yA + yB + yC ] + xB − --------------,yB − -------------- + [ 3 3 ] xA-+-xB-+-xC-- yA-+-yB-+-yC-- + xC − 3 ,yC − 3 = [ ] = x + x + x − 3 ⋅ xA-+-xB-+-xC-,y + y + y − 3⋅ yA-+-yB-+-yC-- = A B C 3 A B C 3 = [0,0].
Wersja PDF