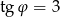/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 1271966

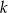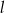Określ wzajemne położenie prostych k i l o równaniach

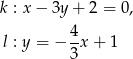
k : x − 3y + 2 = 0 , 4- l : y = − 3 x+ 1
Wersja PDF

Rozwiązanie

Zapisujemy proste w postaci kierunkowej

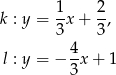
1 2 k : y = -x + --, 3 3 l : y = − 4-x + 1 3

Ponieważ współczynniki kierunkowe tych prostych nie są równe, proste te nie są równoległe. Aby wyznaczyć kąt 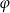φ pod jakim się przecinają, korzystamy ze wzoru:

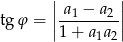
| | ||-a1-−-a2-|| tg φ = |1 + a a | 1 2

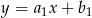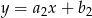dla prostych y = a1x + b 1 i y = a2x + b2 .

W naszej sytuacji

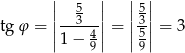
|| 5 || ||5|| tg φ = ||---3--||= ||3|| = 3 |1 − 4| |5| 9 9

Proste przecinają się zatem pod kątem 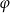φ takim, że tg φ = 3 .  
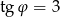Odpowiedź: Proste przecinają się pod kątem 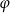φ takim, że tg φ = 3

Wersja PDF