Zadanie nr 1309036
Dane są punkty 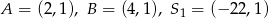 i
i 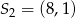 . Odcinek
. Odcinek 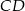 jest obrazem odcinka
jest obrazem odcinka 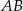 w jednokładności o skali dodatniej i środku
w jednokładności o skali dodatniej i środku 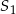 , jak i w jednokładności o skali ujemnej i środku
, jak i w jednokładności o skali ujemnej i środku 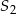 . Oblicz współrzędne punktów
. Oblicz współrzędne punktów 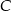 i
i 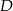 .
.
Rozwiązanie
Wykonujemy szkicowy rysunek – niestety niewiele on nam pomoże, bo wszystkie podane punkty leżą na jednej prostej.
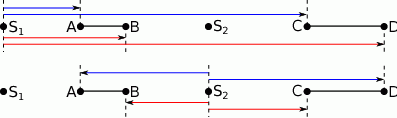
Oznaczmy przez 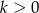 skalę podobieństwa odcinków
skalę podobieństwa odcinków 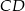 i
i 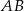 (tzn.
(tzn. 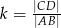 ). W takim razie jednokładność o środku
). W takim razie jednokładność o środku 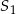 ma skalę
ma skalę 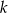 , a jednokładność o środku
, a jednokładność o środku 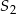 ma skalę
ma skalę 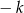 . Jednocześnie, jeżeli pierwsza przekształca punkty
. Jednocześnie, jeżeli pierwsza przekształca punkty 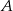 i
i 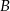 na
na 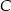 i
i 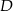 odpowiednio, to druga przekształca
odpowiednio, to druga przekształca 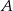 na
na 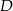 , a
, a 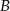 na
na 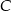 . Te informacje pozwalają wyznaczyć współrzędne punktów
. Te informacje pozwalają wyznaczyć współrzędne punktów 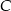 i
i 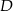 .
.
Oznaczmy 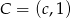 i
i 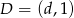 . Mamy zatem
. Mamy zatem
![( −→ −→ ( −→ −→ { S1C = k⋅S 1A { S 2D = −k ⋅S 2A ( −→ −→ ∧ ( −→ − → S1D = k⋅ S1B S 2C = −k ⋅S2B . { { [c+ 22,0] = k ⋅[2 4,0] ∧ [d − 8 ,0 ] = −k ⋅[− 6,0] [d + 22,0] = k ⋅[26,0] [c − 8,0] = −k ⋅[− 4,0].](https://img.zadania.info/zad/1309036/HzadR21x.gif)
Otrzymujemy stąd układ równań.
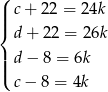
Odejmując od pierwszego równania ostatnie mamy
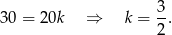
Zatem
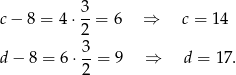
To oznacza, że 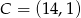 i
i 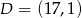 .
.
Odpowiedź: 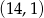 i
i